Моделирование нестационарного теплового процесса

Министерство образования и науки РФ

Федеральное агентство по образованию

Новосибирский Государственный Технический Университет

Кафедра прикладной математики

Лабораторная работа №1

по дисциплине

«Технология математического моделирования

физических процессов»

«Моделирование нестационарного теплового процесса»

Факультет:           ПМИ

Группа:                 ПМ-23

Студенты:             Демин Д.С.,

Липатников Р.Е.

Преподаватели:    Рояк М.Э.

Чернышев А.В.

Новосибирск 2006

Постановка задачи

Найти распределение температуры внутри расчетной области с постоянным источником тепловыделения заданной мощности.

Процесс распределения температуры описывается параболическим уравнением:

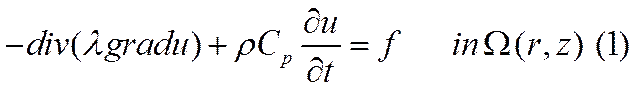
С начальным и краевыми условиями:

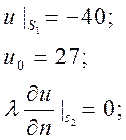
прямоугольная область . На правой границе заданы первые краевые условия: . На правой, верхней и нижней границах заданы однородные вторые условия. Начальное распределение температуры .

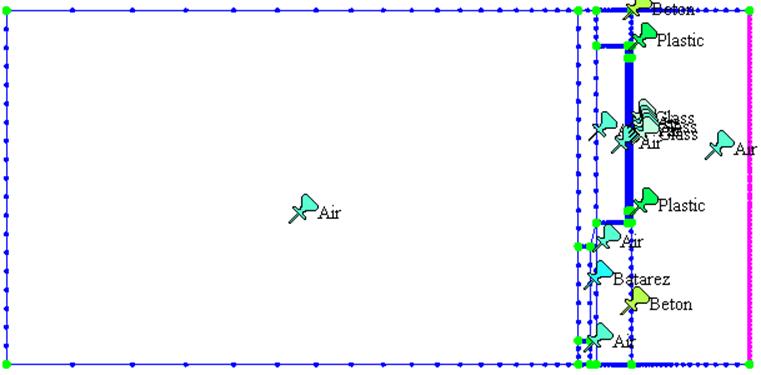
Подобласти  различаются видами материалов: воздух, бетон, пластик, стекло. Для этих сред задаем различные значения плотности  (кг/м3), удельной теплоемкости (Дж/кг*К), теплопроводности. Внутри расчетной области есть источник тепловыделения – батарея. Значения плотности, теплоемкости и теплопроводности для источника задаем как для воздуха и с правой частью равной отношению  мощности (2000 Вт.) к объему источника (0,9715 м3). Для задачи (1) проводим конечноэлементную аппроксимацию  на треугольных конечных элементах. Схема по времени – трехслойная неявная.

Рассмотрим для (1) стационарную задачу (2):

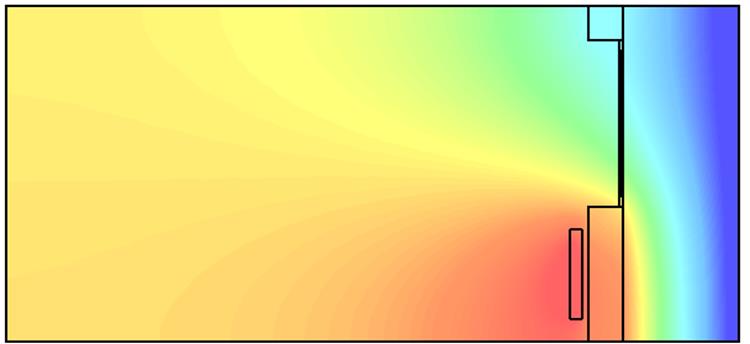
Рис. 1 Распределение температуры стационарной задачи

Минимальная температура равна -40, максимальная – 3011,903.

Для нестационарной задачи (1) рассмотрим временной интервал длительности 1 год  с шагом 1 неделя.

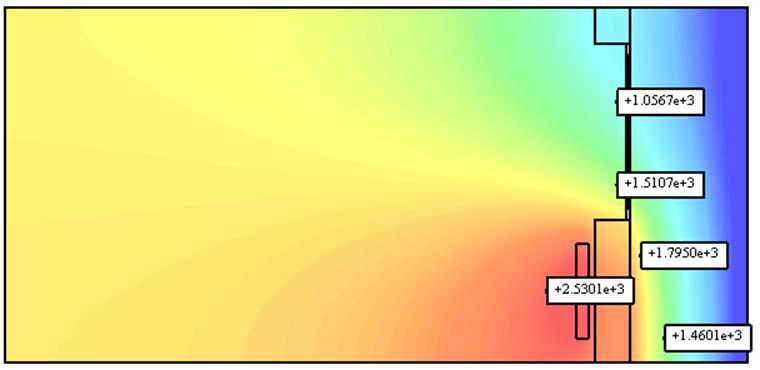
Рис. 2 Распределение температуры при T=1 год

Минимальная температура равна -40, максимальная – 2832,363.

Дробим сетку в 2 раза:

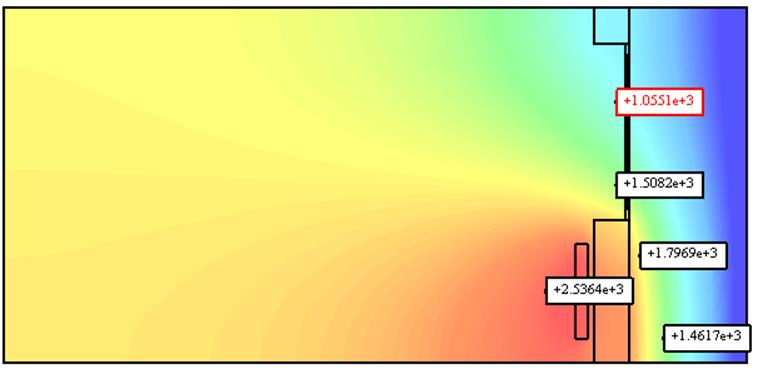
Рис. 3 Распределение температуры при T=1 год

Минимальная температура равна -40, максимальная – 2844,489.

При дроблении пространственной сетки в два раза решение изменяется менее чем на 0,2%, следовательно, дальнейшее сгущение не имеет смысла.

Подробим сетку по времени: интервал длительности 1 год, шаг 0,5 – недели.

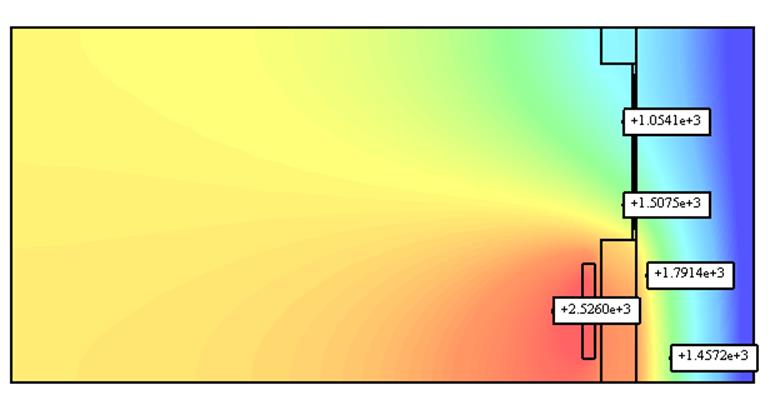
Рис. 4 Распределение температуры при T=1 год

При дроблении временной сетки в два раза решение изменяется менее чем на 0,1%.

Увеличим теплопроводность воздуха в 10 раз

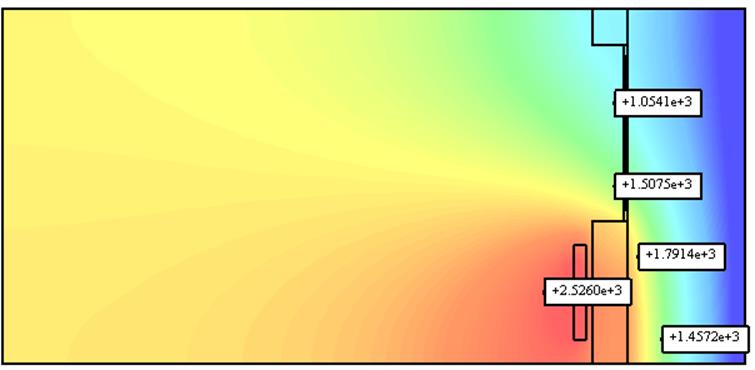
Рис. 5 Распределение температуры при T= 1 год при

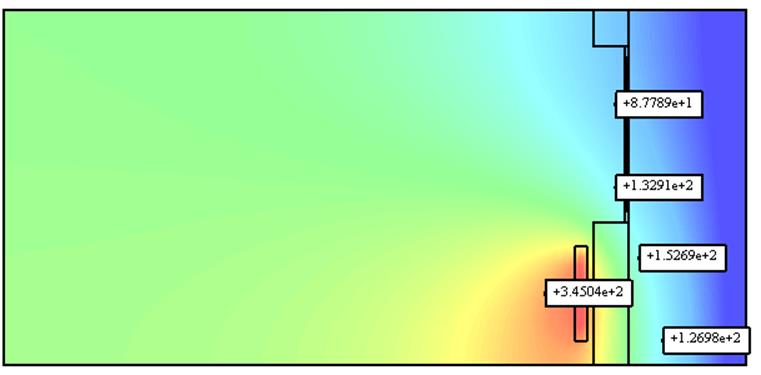
Рис. 6 Распределение температуры при T= 1 год при

Из рисунков видно, что температура в заданных точках стала меньше на порядок.

Увеличим теплоемкость воздуха в 10 раз

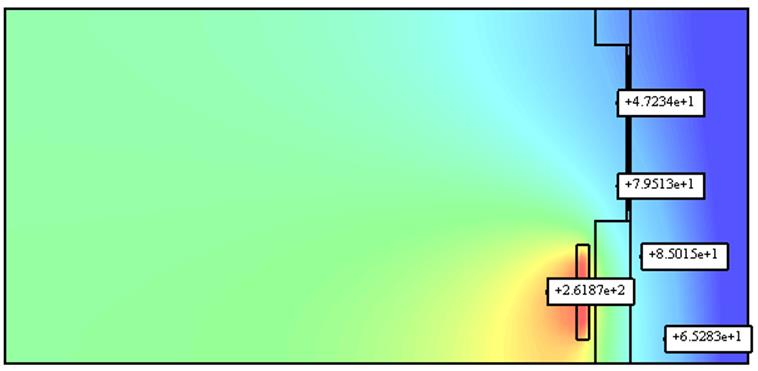
Рис. 7 Распределение температуры при T= 1 год при

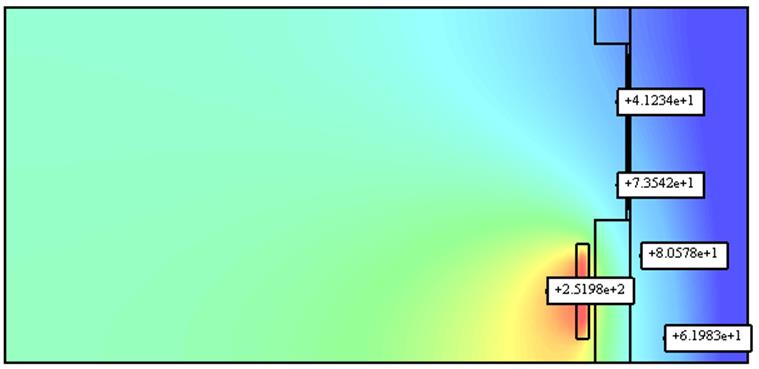
Рис. 8 Распределение температуры при T= 1 год при

Температура в заданных точках уменьшилась на 3%.

Выводы:

1. Решение нестационарной задачи стремится к решению стационарной задачи.
2. При дроблении пространственной сетки в два раза решение изменяется менее чем на 0,2%, следовательно, дальнейшее сгущение не имеет смысла.
3. При дроблении временной сетки в два раза решение изменяется менее чем на 0,1%.
4. При увеличении теплопроводности воздуха в 10 раз температура в заданных точках стала меньше на порядок.
5. При увеличении теплоемкости  воздуха в 10 раз температура в заданных точках уменьшилась на 3%.