





МО РФ
НГТУ
Kафедра прикладной математики
Лабораторная работа №1
по дисциплине «Моделирование и управление в экономике»
на тему «Моделирование дискретных и непрерывных псевдослучайных величин».
Группа: ПМ – 92
Студенты: Терещенко Т., Вамбуева Т., Че Т.
Преподаватель: Самочернов И.В.
1. Цель работы
Изучение программных методов имитации равномерно распределенных псевдослучайных величин на отрезке [0,1]; методов моделирования дискретных и непрерывных псевдослучайных величин; экспериментальное исследование и статистический анализ качества псевдослучайных последовательностей.
2. Задание
2.1
тип программного генератора моделирования псевдослучайных величин – генератор
Ковью: ![]() .
.
Образование
равномерно распределенных псевдослучайных чисел на отрезке [0,1] можно
представить следующим образом 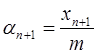 .
.
Исследования:
Зависимость периода от параметров схемы
|
x0 |
m |
период |
|
12 |
27 |
3 |
|
3 |
3Е+7 |
243 |
|
2 |
2Е+6 |
16 |
|
4 |
16 |
1 |
|
9 |
6561 |
81 |
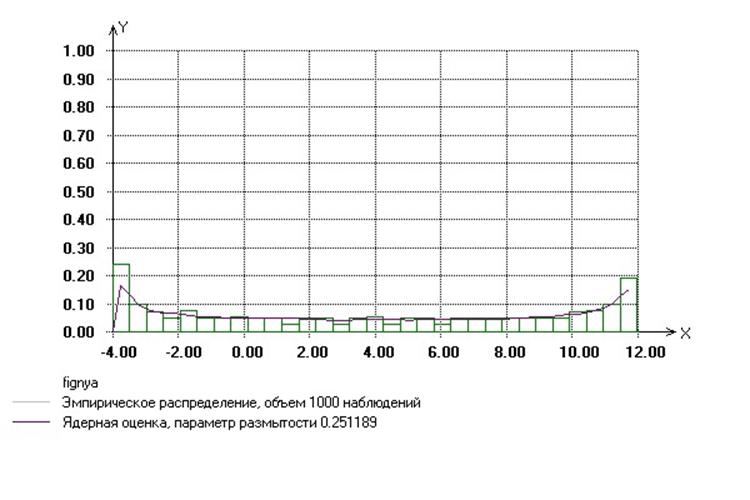
Проверка качества полученных последовательностей
Будем
проверять качество выборок по критерию хи-квадрат, который имеет вид: ![]() где r – это
количество отрезков разбиения, а b
- вероятность ошибки 2-го рода. Положим b
= 0.01.
где r – это
количество отрезков разбиения, а b
- вероятность ошибки 2-го рода. Положим b
= 0.01.
1) X0=2, m=4096, период=1024
|
число разбиений r |
значение |
значение |
|
5 |
0.003906 |
0.088691 |
|
6 |
0.007813 |
0.036632 |
|
10 |
0.023426 |
0.00054 |
|
14 |
0.023438 |
3.607703Е-4 |
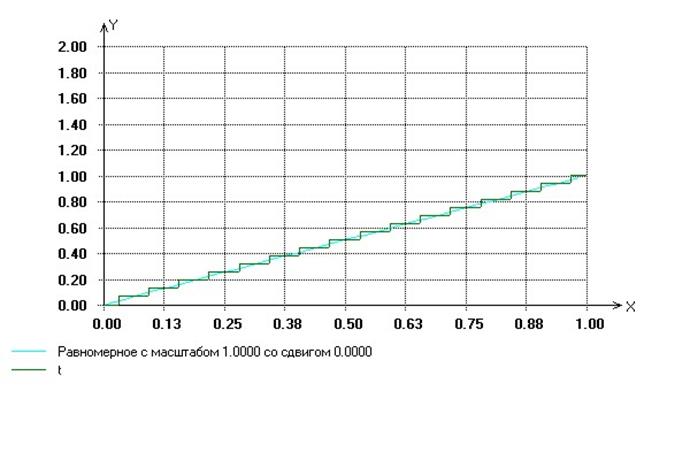
2) Х0=3, М=6561, период=81
|
число разбиений r |
Значение |
значение |
|
7 |
0.148148 |
0.014011 |
|
10 |
0.111111 |
0.00054 |
|
16 |
0.185185 |
2.36187E-5 |
Вывод:
При моделировании равномерно распределенных на отрезке [0,1] псевдослучайных чисел, значение коэффициента m нужно брать достаточно большим, чтобы значения периода сделать как можно больше. Причем период полученной последовательности не должен быть равным нулю. Х0 берем меньше значения m.
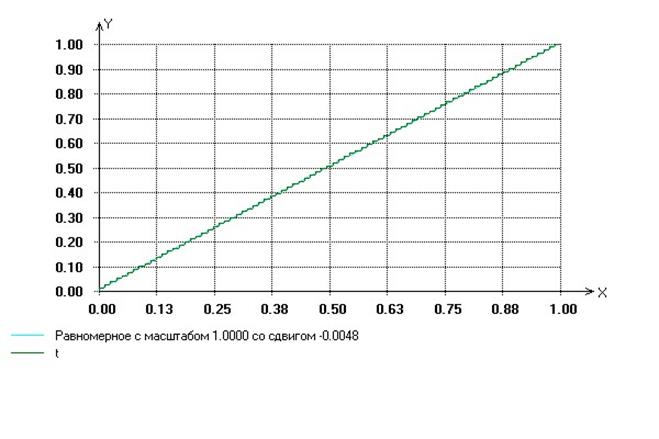
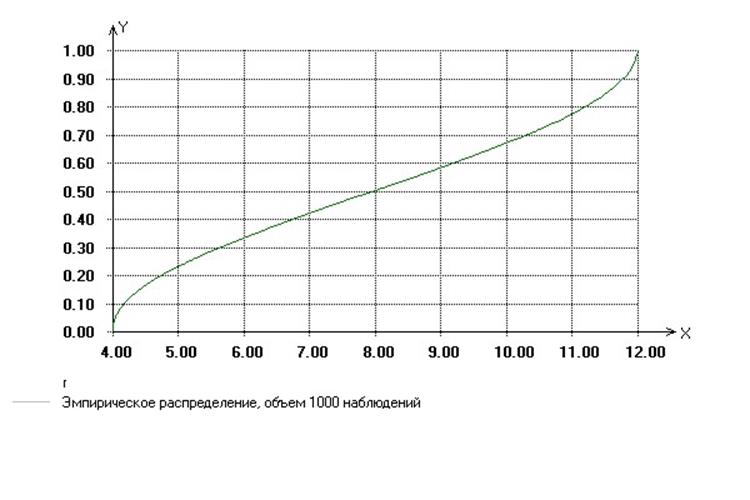
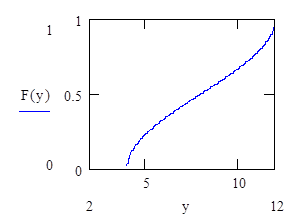
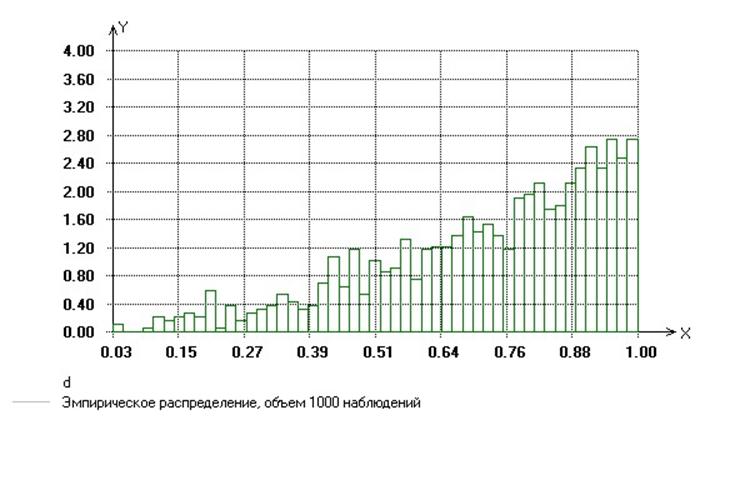
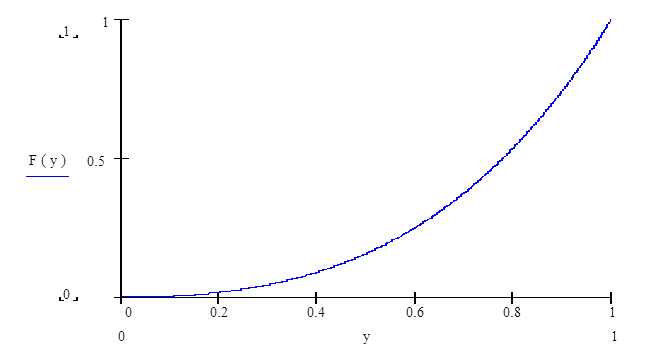
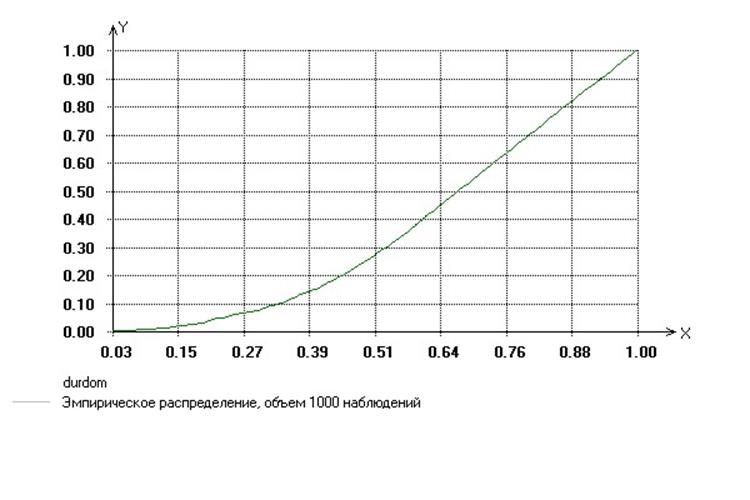
2.2 метод обратных функций
x имеет
плотность распределения: 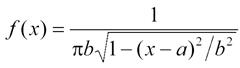 -
монотонная функция
-
монотонная функция
Тогда,
если 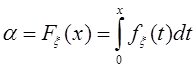 , то можем определить моделирующее значение
для
, то можем определить моделирующее значение
для ![]() x
из уравнения
x
из уравнения ![]() , путем нахождения
, путем нахождения ![]() . Для нашего случая
. Для нашего случая 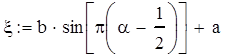
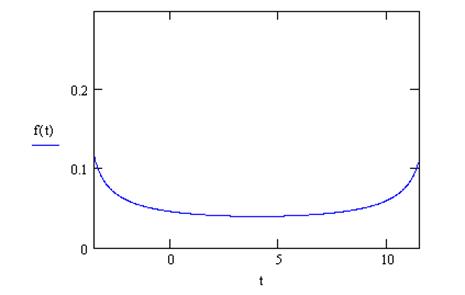
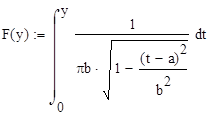
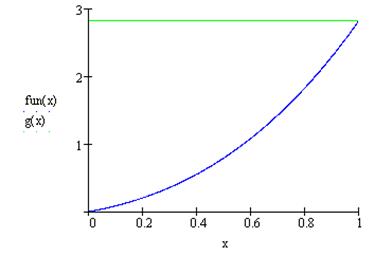
в) метод исключения
Случайная
величина x имеет
следующую плотность распределения: ![]()
Максимум этой функции на области определения достигается в точке х = 1, M=f(1).
Возьмем
в качестве функции g(x), такой что ![]() функцию g(x) = M.
функцию g(x) = M.
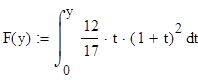
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.