Механизм «условных критических интервалов» Хансена

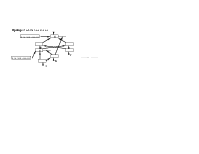
разбить на последовательность коммуникационно-замкнутых слоев, то доказательство ее (частичной) корректности сводится к последовательному доказательству вход-выходных соотношений для каждого слоя. Это существенно упрощает анализ корректности параллельной программы. На рис. показано разбиение процессов Small и Large на КЗ слои.

когерентность параллельной программы.

Для упрощения верификации параллельной программы уже при ее проектировании на нее можно наложить дополнительные требования, облегчающие ее понимание и анализ, и заранее устраняющие некоторые типы возможных ошибок. Одним из таких требований является когерентность параллельной программы.

                    Неформально, требование когерентности означает:

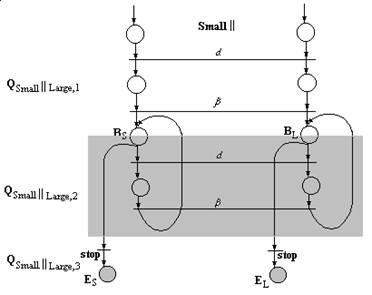
-каждый раз, когда процесс хочет послать сообщение другому процессу, его партнер готов принять это сообщение, т.е., обязательно выходит на оператор приема сообщения;

-каждый раз тогда, когда процесс хочет получить сообщение некоторого типа от другого процесса, его партнер посылает ему это сообщение. При разбиении параллельной проги на КЗ слои : Pi=Q_i,1;Q_i,2;...Q_i,k. К требованию когерентности добавляется: каждая команда взаимодействия обязательно сочетается с некоторой командой взаимодействия из операторов того же самого слоя. Для P=[Small || Large] синхронизация показана на рис.2.

19.Модели параллельно-последовательного программирования. MPMD и SPMD модели программирования. Необходимость явного распараллеливания.

Модель вычислений методом параллельных олераторов

Begin         d1: c:=lg(a);

d2: d:=lg(b);

d3: e:=c+d;

d4: f:=d*d;

d5: g:=e/f end;

Если параллельных реализаций >2 , то алгоритм наз паралельным. Реализации эквивалентны, еслипри выполнение они приаодят к получению одного рез-та. Программа однозначна, если любая допустимая ею вычислительная реализация дает один итот же рез-т. Данную прогу можно представить:

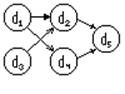
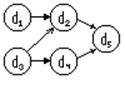
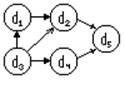
Основным источником параллелизма явл-ся информационная зависимость операторов. Граф инф-ой зависимости совпадает с максимально параллельной реализацией.

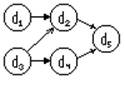
Модель вычислений методом параллельных ветвей: программа разбивается на блоки (сегменты)

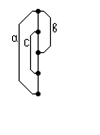Begin d1

[begin d2; [d4,d5], d7] end;

begin d3; d6 end]; d8 end.

Fork (a,b,c) - точка разветвления парал. процессов

Join (a,b,c,…) – точка слияния.

1.  между ветвями нет взаимодействия- харак-я особенность исполнения парал-х ветвей;

2.  после каждого парал-го пучка процессов (яруса) нужны точные указания следующего яруса или разветвления.

MPMD(много программ – много данных). - программа представляет собой совокупность некоторых автономных процессов, функционир-х под управл-м своих собственных программ, взаимод-х посредством стандартного набора библиотечных процедур для передачи и приема сообщений.

SPMD(одна программа – много данных).- все процессы исполняют в общем случае различные ветви одной и той же программы. Такой подход обусловлен тем обстоятельством, что задача м.б. достаточно естественным образом разбита на подзадачи, решаемые по одному алгоритму. На практике чаще всего встречается именно эта модель программирования.

Необходимость явного распараллеливания : 1. Пользователь должен в явном виде указывать стр-ру ; 2.  Пользователь должен явно задавать взаимодействия между парал-ми проц-ми , поэтому языковой уровень явл-ся ниже уровня программы на языке высокого уровня.

21.Ускорение и эффективность вычислений. Закон Амдала.

При достижении ускорения необходимо учитывать  не только архитектурные особенности, но и структуру программы. Рассмотрим алгоритмы Гаусса: t_c- время обработки одной строки, t_p –время приема данных, N- кол-во строк у процессора, k- кол-во компов, взаимодействие асинхронное. 1. [t_c + t_р+( t_р*N+ t_c)*N]* (k-1)+N t_c, при t_c= t_p : t_c*(k*(2+N+N²)- N²-2); 2. K*(N*( t_c + 2*t_р)+(N+1)*N* t_c /2), при t_c= t_p : t_c*k*(3,5N+ N²/2). Если t_c=1, к=4 ,N=100, то t 1-го алгоритма 30406, 2-го 21400 . Т.е. второй алгоритм лучше по времени.

Более эффективный последовательный алгоритм при распараллеливании может стать менее эффективным. Сортировка Хоара последовательная лучше сортировки Бэтчера.

Коэффициент Бэтчера = ; а коэффициент Хоара = . Т.е. параллельный Бэтчер стал лучше.

Закон Амдалла.

 - доля последовательных операций. Чтобы оценить ускорение s, которое может быть получено на р процессах при данном значении f воспользуемся законом Амдалла.

; Независимо от количества процессов в данном случае.

Чтобы ускорить выполнение в q раз необходимо не менее чем в q раз увеличить  часть программы.

22.Событийное управление. Типичные локальные ситуации, которые могут возникнуть, представить сетью Петри. Операции над сетями Петри (присоединения, исключения, итераций, наложения), продемонстрировать примерами.

Механизм событийного управления (условия готовности формируются как логич.функции от некоторых событий) базируется на сетях Петри, позволяет описать более сложные управляющие ситуации, чем механизм последоват.-параллельного управления семафорами и значит порождает более мощные множества параллельных вычислений.

Промоделируем типичные локальные ситуации.

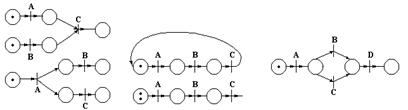
Для описания семантики в классе сетей Петри был выделен класс регулярных сетей, порождающийся из класса элементарных сетей с помощью:

1. присоединение (;): каждое выходное место первого операнда сливается со входным местом операнда справа. Разметки суммируются.

2. объединение (||):

 объединяет две сети, сливая раздельно множество входов и множество выходов сетей каждый с каждым.

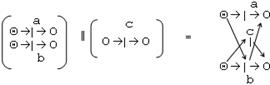3.итерация (*): сливает множество входных и выходных мест сети

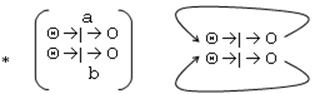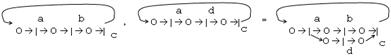4. наложение (,): объединяет переходы мест двух сетей. Одинаковые переходы и дуги сливаются.

23.Потоковое управление (определение). Операции: преобразователь синхронизатор распределитель, селектор, арбитр. Пример реализации этими операциями условного выражения: ifa<bthena+celsea-c

Потоковое управление, в этом случае оператор может выполняться, если готовы все необходимые для него аргументы. Существует неявные. Для того, чтобы обнаружить наличие или отсутствие данных, вводится активная память, которая называется очередью (очередь каналов).

Структура, которая описывается графом, дуги–очереди, вершины–операторы. Когда оператор инициирован из его входных очередей извлекаются данные, а при завершении из выходных результат.

Операции

1. Преобразователь:                  

 

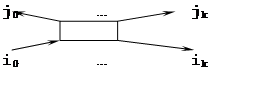Вычисляет результат. Результат выдаётся в стольких элементах сколько входных очередей.

2. Синхронизатор.

Копирует набор данных из входных очередей в выходные

 

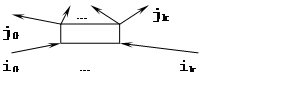3. Распределитель

Имеет 2 входные очереди: основная и вспомогательная. Считывает из основной очереди данные и передаёт очереди, номер которой равен