Методы планирования и анализа в экономических и социологических исследованиях

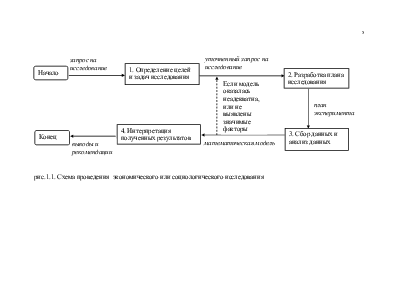
математической модели конечным числом возможных пар { (F₁ ⁱ , F₂ ⁱ ), i=1,..., k }, основываясь на физических соображениях или по соображениям эвристического характера. Задача идентификации модели заключается в выборе среди возможных пар функций подходящей пары и в последующем оценивании соответствующего вектора параметров q в выбранной паре.

Пусть некоторый процесс характеризуется наблюдаемыми переменными: m-мерным выходным вектором отклика y и входным l₁-мерным вектором  факторов u. Будем полагать, что последовательность факторов (управляющих воздействий) {u(t), t =0, 1,..., N-1} измеряется без случайных помех, таким образом, управление детерминировано.

В общем случае, дискретная линейная модель описывается стохастическим разностным уравнением:

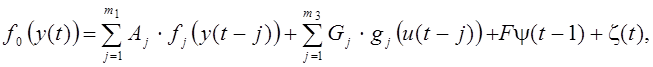                 (2.2)

в котором динамическое поведение y(t) целиком определяется его прошлыми значениями, прошлыми значениями управляющего вектора u и вектором возмущений z (t), не зависящим от прошлых значений управляющих и выходных сигналов.

Вектор y(t), размерности l₂,  составлен из описывающих детерминированный тренд функций, которые при построении модели процесса считаются полностью известными. Подходящие детерминированные функции времени обычно подбираются в результате просмотра эмпирических данных и их характеристик, а также применения процедур проверки гипотез.

Вектор-функции , полагают детерминированными и полностью известными. Часто полагают функции равными: .

Поскольку эти функции могут быть нелинейными, уравнение (2.2) нелинейное по входящим в него наблюдениям, но линейно по параметрам – элементам матриц A_j (j=1,..., m₁ ),  G_j  (j=1,..., m₃),  F.

Обозначив оператор единичной задержки D, D( y( t) ) = y( t- 1 ), уравнение авторегрессионного процесса  (2.2) с использованием матричных многочленов  можно записать в компактной форме:

       (2.3)

где

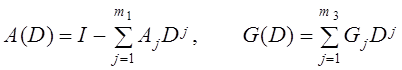.                 (2.4)

Возмущения  z(×) в некоторых случаях можно предполагать последовательностью независимых случайных величин, при таком подходе (2.3) описывает авторегрессионную модель. Однако, такое предположение в некоторых ситуациях может не выполняться. Поэтому в более общем случае, принимают предположение, что z (t) - процесс с нулевым математическим ожиданием и конечным временем корреляции:

, который можно описать процессом в виде скользящего среднего:

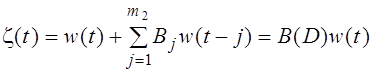,                                     (2.5)

где

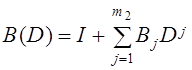,    ,      (2.6)

d_ij - символ Кронекера. Таким образом,  {w(×)} - белая последовательность независимых случайных величин с нулевым средним.

Подставляя представление (2.5) для возмущений z (t) в уравнение процесса (2.3), получаем окончательный вид модели:

              (2.7)

с процессом {w(×)} , удовлетворяющим условиям (2.6).

Модель, описываемую уравнением (2.7), будем называть ARMAX-моделью [7], поскольку в ней представлена зависимость значения y(t) от предыдущих значений выходного сигнала (AR-элементы), процесса скользящего среднего (MA- элементы) и от управляющих воздействий (X- элементы).

Уравнение (2.7)  можно представить в матричном виде:

,                                               (2.8)

Векторный параметр  q  = (q ₁ ^T, q ₂ ^T,..., q _m^T)^T имеет размерность n=m× n_z, его составляют вектора  q_i(i=1,2,...,m)размерности n_z.  Коэффициенты вектора q_i (i=1,2,..., m) представляют собой элементы  i-х строк матриц A_j (j=1,..., m₁ ),  G_j  (j=1,..., m₃),  F,  B_j  (j= 1,..., m₂), то есть параметры, которые явно участвуют в вычислении выходного сигнала y_i(t)  по формуле (2.7).

Матрица наблюдений Z(t-1) имеет размерность mх(m× n_z):

.

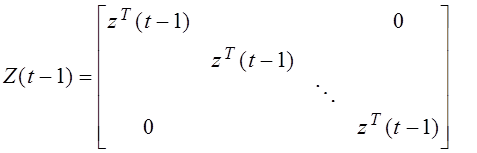Вектор-строка  z^T (t-1) имеет размерность n_z =m×m₁+l₁×m₂+l₂+m× m₃ .

В вектор z^T (t-1) объединены наблюдения, необходимые для вычисления y_i(t),  i=1,2,...,m, по формуле (2.7):

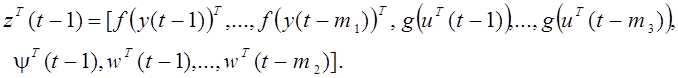   (2.9)

В случае модели с одним выходом (m=1) уравнение (2.8) принимает вид:

.                                 (2.10)

Следует заметить, что составить  вектор z (t-1) по выражению (2.9)  и, следовательно, матрицу z(t-1) для (2.8) возможно только начиная с некоторого момента времени, когда накопятся все необходимые наблюдения. Обозначим этот момент времени  nmax:         nmax = max (m₁, m₂, m₃) , где m₁- число предыдущих значений выходного сигнала («глубина» AR-зависимости), от которых зависит текущее значение y(t); m₂ - глубина процесса