МО РФ
НГТУ
Лабораторные работа №3
по дисциплине
«Методы моделирования»
Кафедра: ПМт
Факультет: ПМИ
Группа: ПМ-86
Студенты: Кочанов М.В.
Рощина Т.Е.
Юркевич А.В.
Преподаватели: Тимофеев В. С.
Тишковская С. В.
Новосибирск 2001
1. Задание
·
Найти методом
обратной функции моделирующее выражение для случайной величины ![]() , имеющей заданную плотность распределения:
, имеющей заданную плотность распределения:
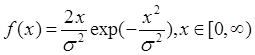 ; (1)
; (1)
·
Найти
моделирующее выражение для случайной величины ![]() ,
имеющую заданную плотность распределения, по методу обратной функции, когда
,
имеющую заданную плотность распределения, по методу обратной функции, когда ![]() немонотонна:
немонотонна:
![]() ; (2)
; (2)
·
Написать
алгоритм моделирования случайной величины ![]() ,
распределенной с плотностью
,
распределенной с плотностью ![]() с использованием
порядковых статистик:
с использованием
порядковых статистик:
![]() ; (3)
; (3)
·
Написать
алгоритм моделирования случайной величины ![]() с
заданной плотностью распределения
с
заданной плотностью распределения ![]() :
:
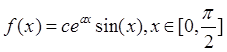 ; (4)
; (4)
·
Написать
алгоритм моделирования случайной величины ![]() с
заданной плотностью распределения по методу суперпозиции:
с
заданной плотностью распределения по методу суперпозиции:
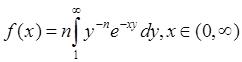 ; (5)
; (5)
·
Написать
алгоритм моделирования случайной величины ![]() с
плотностью
с
плотностью ![]() по методу исключения:
по методу исключения:
![]() . (6)
. (6)
2. Постановка задачи
Исходя из методов указанных для
заданий (1)-(6) были получены следующие алгоритмы моделирования случайной
величины ![]() :
:
(1): ![]() ; (1*)
; (1*)
(2): 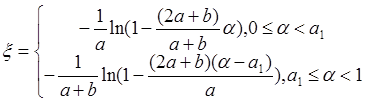 ,
,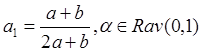 ;(2*)
;(2*)
(3):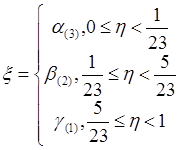 ,
, ![]() ,
, 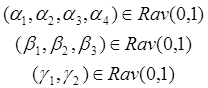 ;(3*)
;(3*)
(4):
1) 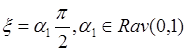
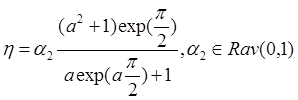 (4*)
(4*)
2) Если ![]() , то
, то ![]() , иначе 1);
, иначе 1);
(5): ![]() ; (5*)
; (5*)
(6): 1) ![]()
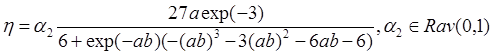
2) Если ![]() , то
, то ![]() , иначе 1).
, иначе 1).
Т.к. в задании № 4 метод моделирования не был указан, то моделирование осуществлялось по методу исключения.
Для оценки качества моделируемой
выборки будем использовать критерий ![]()
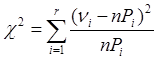 , (7)
, (7)
где n – объем выборки, ![]() -
количество элементов выборки, попавших в i-ый интервал разбиения, Pi – вероятность попадания в i-ый интервал, а r – количество интервалов.
-
количество элементов выборки, попавших в i-ый интервал разбиения, Pi – вероятность попадания в i-ый интервал, а r – количество интервалов.
Для вычисления Pi, там где возможно, а именно в заданиях (1)-(4),(6), было получено явное выражение для функции распределения, а в для задания (5), чтобы определить значения функции распределения применялось численное интегрирование (метод Гаусса-2).
Исследования качества полученных выборок производилось при r=16 (количество степеней свободы 15).
Так как все алгоритмы моделирования случайных величин с функциями распределения (1)-(6) были сведены к моделированию равномерно распределенных на отрезке [0,1] случайных величин, то в качестве генератора последних использовалась следующая схема:
![]() (8)
(8)
3. Результаты
![]() , где
, где ![]() -
вероятность отвергнуть верную гипотезу.
-
вероятность отвергнуть верную гипотезу.
(1):![]() =1
=1
|
Объем выборки |
Статистика
|
Квантиль |
|
|
Знач. |
P |
||
|
500 |
3.358886 |
4.60092 |
.995 |
|
1200 |
2.071985 |
4.60092 |
.995 |
(2):a=2,b=3,c=a(a+b)/(2a+b)
|
Объем выборки |
Статистика
|
Квантиль |
|
|
Знач. |
P |
||
|
500 |
6.331054 |
7.26094 |
.950 |
|
1200 |
8.504591 |
8.54676 |
.900 |
(3):c=12/23
|
Объем выборки |
Статистика
|
Квантиль |
|
|
Знач. |
P |
||
|
500 |
7.422883 |
8.54676 |
.900 |
|
1200 |
7.128061 |
7.26094 |
.950 |
(4):a=1,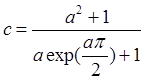
|
Объем выборки |
Статистика
|
Квантиль |
|
|
Знач. |
P |
||
|
500 |
2.996870 |
4.60092 |
.995 |
|
1200 |
8.434340 |
8.54676 |
.900 |
(5):
|
Объем выборки |
Статистика
|
Квантиль |
|
|
Знач. |
P |
||
|
500 |
2.527668 |
4.60092 |
.995 |
|
1200 |
8.533080 |
8.54676 |
.900 |
(6):a=1,b=3,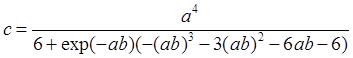
|
Объем выборки |
Статистика
|
Квантиль |
|
|
Знач. |
P |
||
|
500 |
3.163118 |
4.60092 |
.995 |
|
1200 |
3.060095 |
4.60092 |
.995 |
4. Анализ результатов
(1):
Гипотеза ![]() принимается
в обоих случаях с высокой вероятностью.
принимается
в обоих случаях с высокой вероятностью.
(2):
Гипотеза ![]() принимается
в обоих случаях с достаточно высокой вероятностью. Но в этом случае с
увеличением объема выборки произошло некоторое ухудшение ее качества, это
можно объяснить тем, что параметры схемы (8) оказались более эффективными для
выборки объема 500, нежели для 1200.
принимается
в обоих случаях с достаточно высокой вероятностью. Но в этом случае с
увеличением объема выборки произошло некоторое ухудшение ее качества, это
можно объяснить тем, что параметры схемы (8) оказались более эффективными для
выборки объема 500, нежели для 1200.
(3):
Данный метод позволил смоделировать выборки приличного качества. Это объясняется тем, что для генерации наборов случайных величин с объемами 2,3 и 4 использовался один генератор, и из выборки построенной этим генератором последовательно извлекались 2,3 или 4 элемента, которые в общем случае могли и не быть равномерно распределенными.
(4):
Гипотеза ![]() принимается
в обоих случаях с достаточно высокой вероятностью. Но в этом случае с
увеличением объема выборки произошло некоторое ухудшение ее качества, это
можно объяснить тем, что параметры схемы (8) оказались более эффективными для
выборки объема 500, нежели для 1200.
принимается
в обоих случаях с достаточно высокой вероятностью. Но в этом случае с
увеличением объема выборки произошло некоторое ухудшение ее качества, это
можно объяснить тем, что параметры схемы (8) оказались более эффективными для
выборки объема 500, нежели для 1200.
(5):
Гипотеза ![]() принимается
в обоих случаях с достаточно высокой вероятностью. В данном случае с
увеличением объема выборки опять произошло некоторое ухудшение ее качества,
причины можно объяснить также как и в ситуации с (2) и (4).
принимается
в обоих случаях с достаточно высокой вероятностью. В данном случае с
увеличением объема выборки опять произошло некоторое ухудшение ее качества,
причины можно объяснить также как и в ситуации с (2) и (4).
(6):
Гипотеза ![]() принимается
в обоих случаях с высокой вероятностью.
принимается
в обоих случаях с высокой вероятностью.
5. Вывод
При помощи всех методов были получены выборки хорошего качества. Так как в основе каждого метода лежит генерация равномерно распределенных случайных чисел, то качество выборок, имеющих произвольное распределение, напрямую зависит от качества последовательностей чисел, имеющих равномерное распределение. По вычислительным затратам лучше являются методы: исключения и порядковых статистик.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.