Методы линеаризации уравнений.

Методы линеаризации уравнений.

1) Нелинейная функция является аналитической в рабочей области и ее можно разложить в ряд Тейлора.

Простейшим методом изучения нелинейных систем является линеаризация. Суть ее состоит в том, что нелинейная система заменяется эквивалентной линейной. Очевидно, что линеаризованная модель не может заменить полностью нелинейную систему, но в некоторых отношениях поведение линеаризованной модели может быть вполне идентичным поведению нелинейной системы. Т.о., имеется возможность применять некоторые хорошо разработанные методы анализа линейных систем для изучения линеаризованной системы.

Обычно при описании элементов непрерывного действия используются переменные состояния x(t), связанные с входными U(t) и выходными y(t) сигналами с помощью следующих соотношений:

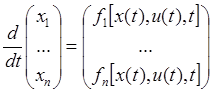 (1)

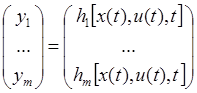 (2)

Будем считать (1)-(2) нелинейной,  если в ней переменные состояния присутствуют не только в линейной форме, но и в форме произведений, целой (дробной) степени координат и трансцендентной функции от них. Во многих элементах нелинейная зависимость не удается выразить аналитически, тогда ее представляют в виде графиков или таблиц.

Линеаризуем модель (1)-(2) по этому методу, при условии малости приращений  относительно положения равновесия (т.е., когда переходный процесс завершен): . Тогда представляем:,  (- приращение). Аналогично:,  ( r – размерность вектора u). Тогда переходим к уравнениям вида:

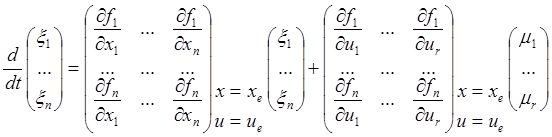 (1*)

Т.о. линеаризовали (1). То же самое проделаем с (2). Запишем , где

Тогда имеем:

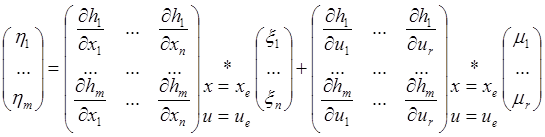 (2*)

Если провести линеаризацию относительно опорной траектории прогнозируемого движения с параметром (н – значит номинальное): . Тогда   

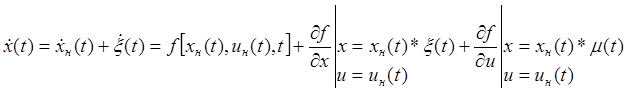
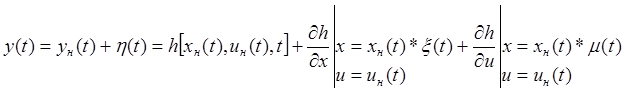
2) Нелинейные характеристики не могут быть описаны математически, а задаются в графической форме соответствующими зависимостями.

(график)

(1,2,3 – режимы работы)

В данном методе график заменяется касательной. Т.е., та модель, которую должны получить:

Если точка фиксирована, то надо смотреть приращения и .

3). Вместо непосредственного определения частных производных, вводим переменные в исходные нелинейные уравнения:

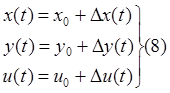
Все слагаемые, стоящие в правых частях полученных выражений, разобьем на три группы:

-  не содержащие приращения Dx и Du;

-  содержащие приращения Dx и Du в виде простых множителей;

-  содержащие произведения или степени приращения.

Полагая Dx и Du маленькими по сравнению с соответствующими координатами опорной траектории x₀,u₀ можно считать слагаемые третьей группы практически равными нулю. Слагаемые первой группы будут определять опорное движение, а слагаемые второй группы – движение в отклонениях Dx и Du от опорной траектории.

МНК

Есть функция ; М – рабочая точка, в которой надо линеаризовать f , M=(x_10,…x_n0).

y₀ = f(M). Предположим, что переменная y определена в N выборочных точках вблизи М, N>n. Т.е., y_i = f(x_1i, x_2i, …, x_ni). Линеаризованная модель, имеем вид: (13)  Надо найти а_i. Составим сумму квадратов отклонений для выборочных точек, используя коэффициенты линеаризованной модели.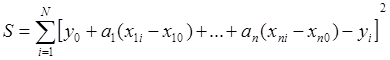. (14) Необходимое условие минимума суммы квадратов (14) в том, что все частные производные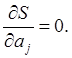  

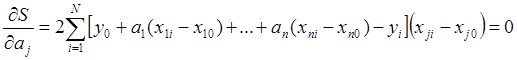
Тогда запишем j-ое уравнение СЛАУ:

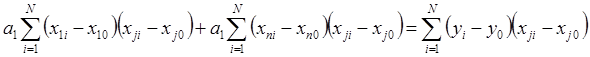 (15) j = 1,..,n

Коэффициенты линеаризации a_j можно определить из системы (15), если выборка корректна, т.е. det ¹0.

Гармоническая линеаризация.

Выполняется в частотной области, при этом нелинейный элемент заменяется линейным, эквивалентным относительно основной составляющей.

Пусть нелинейный преобразующий элемент возбуждается синусоидальным входным сигналом: u(t) = U*sinwt. Выходной сигнал y=f(u) является периодическим. Его основная частота совпадает с частотой сигнала.

Опр.Описывающей функцией называется комплексно-значная функция: Z(u,iw) = X(u,w) + iY(u,w). Определяется как отношение комплексной амплитуды W(u, iw) – основной составляющей выходного сигнала к амплитуде U синусоидального входного сигнала.

Разложим в ряд Фурье сигнал, полученный на выходе нелинейного элемента:

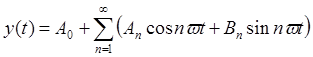, где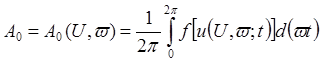

,

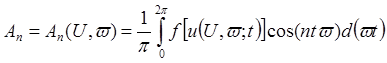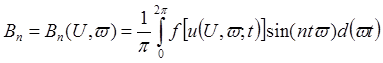
Комплексная амплитуда W(u, iw) основной составляющей выходного сигнала, будет равна:   определяется как: ,

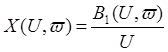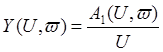
В методе описывающих функций в разложении (18) принимаются во внимание только постоянная и основная составляющие выходного сигнала. Т.е., считают, что высшие гармоники подавляются линеаризованным элементом:

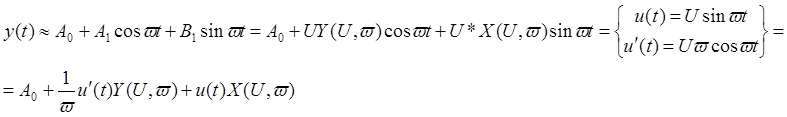
Статистическая линеаризация.

Метод статистической линеаризации применяется в тех случаях, когда сигнал (на входе нелинейного элемента) – случайный (для простоты обычно предполагается, что система имеет нормальное распределение).

НЭ

U(t)®               ®y(t)

, , , где - шум.

Статистическая линеаризация состоит в определении приближением линейной зависимости между выходными и входными переменными, которая соответствует указанной ситуации.

При статистической линеаризации путем замены нелинейного элемента соответствующим линейным, стремятся получить с достаточной точностью полезную составляющую выходного сигнала m_y(t) и среднеквадратического отклонения s_y(t).

1) Первый метод.

Нелинейная зависимость y = f(u) между выходной y и входной u переменными заменяется приближенным линейным соотношением: , где  - идеальный выходной сигнал линеаризованного элемента, - полезная составляющая идеальной выходной переменной , - эквивалентный статистический коэффициент усиления нелинейного элемента по отношению к шуму. Связь составляющей  с полезной входной составляющей  задается с помощью характеристики нелинейного элемента. Для нелинейности с центрально-симметричной характеристикой: , где - эквивалентный статистический коэффициент усиления нелинейного элемента по отношению к математическому ожиданию. Необходимо определить  Их можно найти из предположения, что МО  и среднеквадратическое отклонение  идеального сигнала  должны соответствовать МО m_y и среднеквадратическому отклонению s_y действительной выходной переменной.

, ,

,

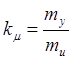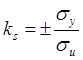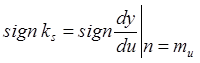
2) Второй метод.

Статистическая линеаризация осуществляется с помощью минимизации среднего квадрата разности между реальным y и идеальным  сигналами:

,

, ,

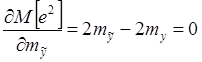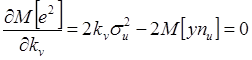
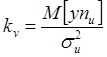
Можно составить матрицу Гессе: 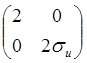 – ее главные миноры > 0, т.о., в данной точке (точке, представленной в виде (36)) будет минимум.