Задание: Реализовать метод простой итерации для задачи:
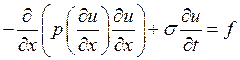
квадратичные базисные функции, первые и вторые краевые
условия, неявная двухслойная схема, ![]() считать постоянной на
КЭ.
считать постоянной на
КЭ.
Решение:
Решая нестационарную задачу 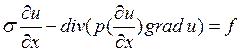 ,
будем аппроксимировать по времени решение используя схему:
,
будем аппроксимировать по времени решение используя схему: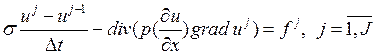
Для каждого ![]() получаем матричное
уравнение вида:
получаем матричное
уравнение вида:
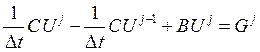
Считая ![]() известным, получаем СЛАУ
для вектора неизвестных
известным, получаем СЛАУ
для вектора неизвестных ![]() :
:
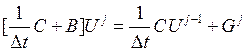
Далее при нахождении матрицы 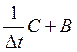 возникает
необходимость посчитать матрицу
возникает
необходимость посчитать матрицу
![]() , а именно
, а именно
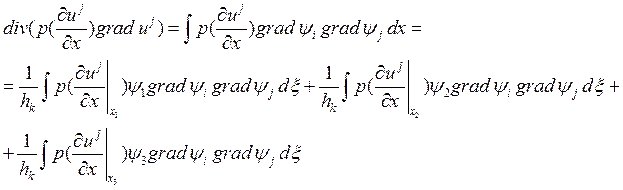
Окончательно для подсчета выражения понадобится найти 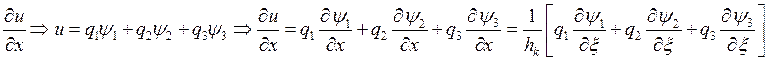 .
.
Далее
решая нестационарную задачу, будем аппроксимировать по времени решение используя
схему: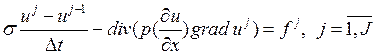
Для
каждого ![]() получаем матричное уравнение вида:
получаем матричное уравнение вида:
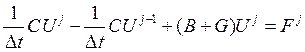
Считая
![]() известным, получаем СЛАУ для вектора
неизвестных
известным, получаем СЛАУ для вектора
неизвестных ![]() :
:
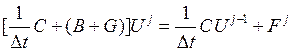
Поскольку базис- квадратичные крышки, т.е с учетом замены 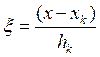 получаем систему функций на каждом конечном элементе вида:
получаем систему функций на каждом конечном элементе вида:
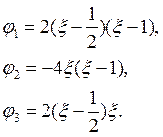
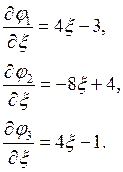
Учитывая все описанное, выше получаем матрицу жесткости вида:
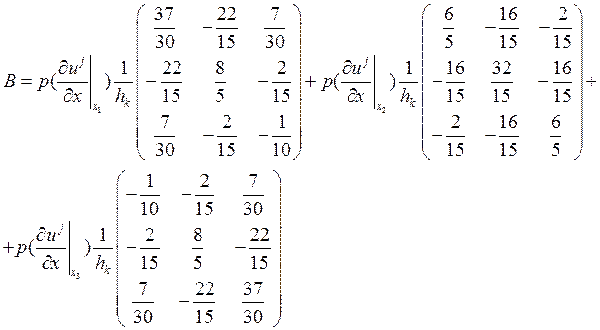
Отдельно для нахождения 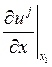 посчитаем
выражение:
посчитаем
выражение:
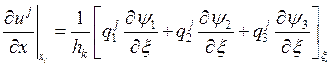
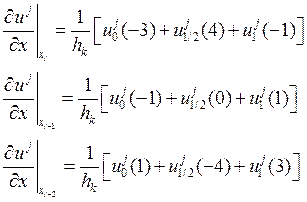
Матрица массы ![]() будет иметь вид:
будет иметь вид:
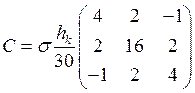
И, наконец, вектор правой части мы будем считать, как
произведение матрицы массы на вектор значений функции ![]() в
узлах сетки, т.е.
в
узлах сетки, т.е. 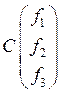 .
.
Далее взяв начальное приближение ![]() и
построив матрицу жесткости на данном временном слое, получаем матрицу СЛАУ вида
и
построив матрицу жесткости на данном временном слое, получаем матрицу СЛАУ вида
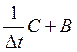 . Теперь определим правую часть
. Теперь определим правую часть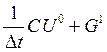 , умножив матрицу массы на вектор
начального приближения
, умножив матрицу массы на вектор
начального приближения ![]() и посчитав вектор
и посчитав вектор ![]() на данном временном слое и т.д.
на данном временном слое и т.д.
Краевые условия будем учитывать следующим образом: для учета
первых краевых будем ставить на диагональ матрицы “большое число”, а на
соответствующее место в векторе правой части большое число, умноженное на
значение функции-решения в узле; для учета вторых краевых 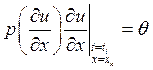 будем аппроксимировать их как при
построении матрицы жесткости:
будем аппроксимировать их как при
построении матрицы жесткости:
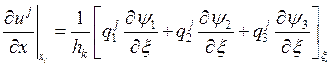 .
.
Тестирование:
Шаг по времени будем выбирать не равномерный, а пространственный равномерным.
:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.