Метод обратной функции моделирующего выражения для случайной величины

Министерство образования РФ

НГТУ

Кафедра ПМт

Индивидуальная работа №1

дисциплина: Моделирование и управление в экономике

Факультет: ПМИ

Группа: ПМ-15

Студент: Казыгашев К.

Преподаватель: Цой Е.Б.

Новосибирск.

2005г.

Условие задач:

1.       Найти методом обратной функции моделирующее выражение для случайной величины  , имеющей заданную плотность распределения: и)      

2.       Найти моделирующее выражение для случайной величины  , имеющей заданную плотность распределения, по методу обратной функции, когда  немонотонна: д)      

3.       Написать алгоритм  моделирования случайной величины  , распределенной по закону , с использованием порядковых статистик: в)      

4.       Написать алгоритм  моделирования случайной величины  , имеющей указанную плотность распределения : б)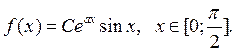      

5.       Написать алгоритм моделирования случайной величины  при помощи метода суперпозиции:

г)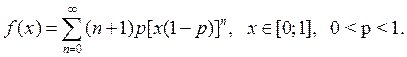      

6.       Написать алгоритм моделирования случайной величины  по методу исключения:

е)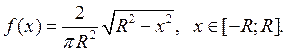      

Задание №1:

Найти методом обратной функции моделирующее выражение для случайной величины  , имеющей заданную плотность распределения: и)      

Решение:

Из условия нормировки функции распределения найдем константу :

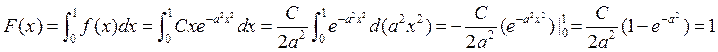, т.е. , т. обр. 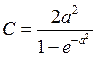 при условии .

И так,  плотность функции распределения имеет вид:

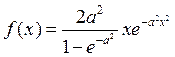, найдем явный вид самой функции распределения:

.

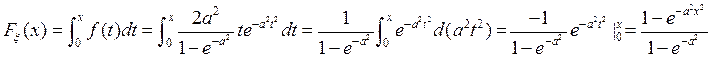Поскольку функция распределения является строго непрерывной и монотонной на области определения: , то можно использовать метод обратной функции:

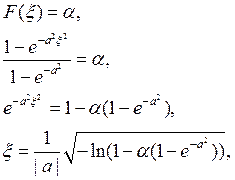
где

Ответ:

Моделирующее выражение для случайной величины  имеет вид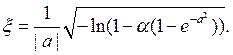

Задание №2:

Найти моделирующее выражение для случайной величины  , имеющей заданную плотность распределения, по методу обратной функции, когда  немонотонна: д)      

Решение:

Из условия нормировки функции распределения определим константу :

,

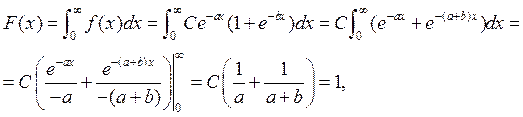
т. обр. .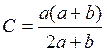

И так,  плотность функции распределения имеет вид:

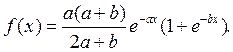 Пусть 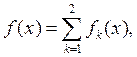 где . Обозначим 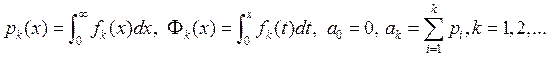 Случайная величина при  имеет плотность распределения .

Пусть 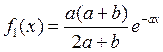 и 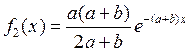. Отсюда вычисляем :

,

,

,

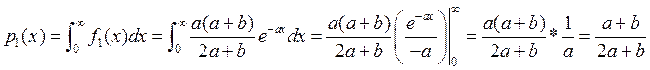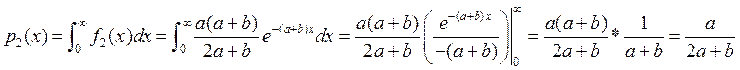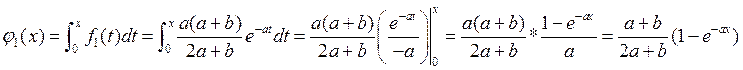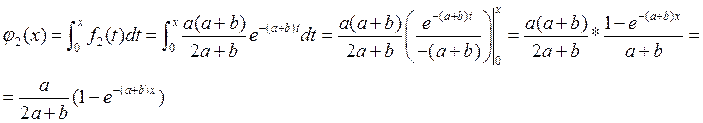
Вычислим значения границ интервалов: , и :

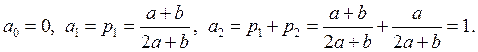
Вычислим значения моделирующих функций на этих двух интервалах.

1)

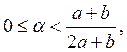
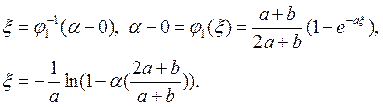
2)

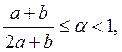
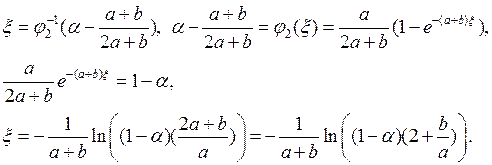
Ответ:

Моделирующее выражение для случайной величины  имеет вид:

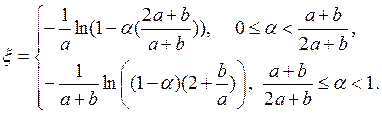
Задание №3:

Написать алгоритм  моделирования случайной величины  , распределенной по закону , с использованием порядковых статистик: в)      

Решение:

Из условия нормировки функции распределения определим константу :

,

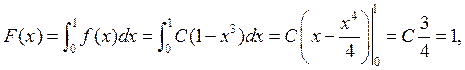 т. обр. .

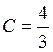И так,  плотность функции распределения имеет вид:

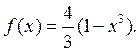
Поскольку в полиноме присутствуют коэффициенты при  степенях  меньше 0, приведем полином к виду полинома Бернштейна:

.

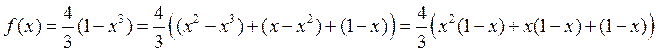Плотность распределения  порядковой статистики равномерного распределения задается в виде: Вычислим и :

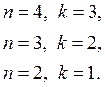
Вычислим коэффициенты полинома Бернштейна:

.

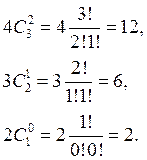
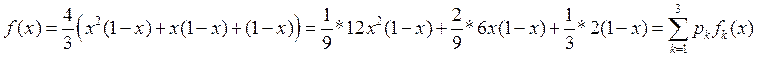Из этой формулы выпишем, какие порядковые статистики понадобятся и с какими вероятностями они должны быть приняты:

1)

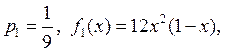
2)

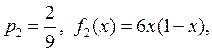
3)

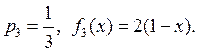
Алгоритм моделирования имеет следующий вид:

1.       Генерируем псевдослучайное число

2.       Интервал  разбивается искомыми вероятностями на 3 интервала. Определяем интервал (его номер ), к которому принадлежит .

3.       Генерируем, в соответствии с номером интервала,  случайных величин (  ) .

4.       Упорядочиваем по возрастанию.

5.       Выбираем наименьшее из них: .

Задание №4:

Написать алгоритм  моделирования случайной величины  , имеющей указанную плотность распределения : б)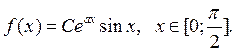      

Решение:

Из условия нормировки функции распределения определим константу :

,

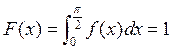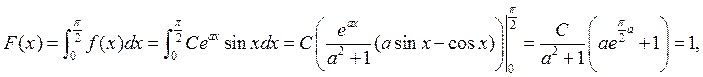
т. обр. .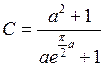

И так,  плотность функции распределения имеет вид:

.

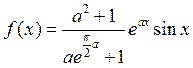Поскольку видно, что метод обратной функции не дает решения через элементарные функции, то  используем метод исключения.

Ограничим плотность функции распределения  сверху константой : пусть 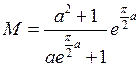, это ограничение в наиболее простом варианте.

Алгоритм моделирования имеет следующий вид:

1.       Генерируем два  числа

2.       Вычисляем

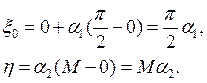
3.       Если  то возвращаемся на шаг 1, иначе  - и есть результат.

Задание №5:

Написать алгоритм моделирования случайной величины  при помощи метода суперпозиции:

г)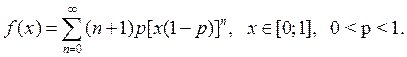      

Решение:

Представим  плотность функции распределения 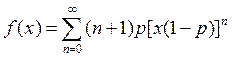 в следующем виде:

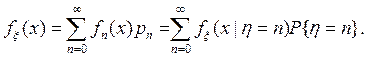
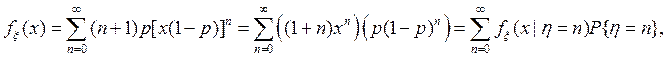 где

 и .

Тогда из условного распределения плотности вычислим ее функцию:

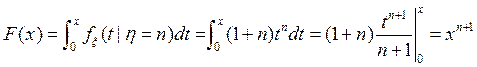, т.е. , где

Суть алгоритма состоит в том, что выбирается случайная дискретная величина , при выполнении равенства  вычисляем , где 

Если выборочные значения  рассматривать в порядке возрастания, то получим случайные величины   - порядковые статистики, распределенные равномерно на отрезке .

Алгоритм моделирования имеет следующий вид:

Задан исходный параметр: .

1.       Генерируем случайное число .

2.       Пусть , вычисляем .

3.       Вычисляем .

4.       Если , то вычисляем , если , то , возвращаемся на шаг 3;

если , то на шаг 5.

5.       Искомая  величина .

Задание №6:

Написать алгоритм моделирования случайной величины  по методу исключения:

е)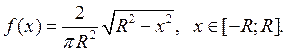      

Решение:

Ограничим плотность функции распределения  сверху константой : 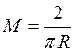- это ограничение в наиболее простом варианте.

Тогда построим алгоритм моделирования, аналогичный в задаче№4.

Алгоритм моделирования имеет следующий вид:

1.       Генерируем два  числа

2.       Вычисляем

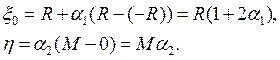
3.       Если  то возвращаемся на шаг 1, иначе  - и есть результат.