



Министерство образования Российской Федерации
Новосибирский Государственный Технический Университет
Индивидуальная работа №1
по дисциплине «Моделирование и управление в экономике»
Факультет: ПМИ
Группа: ПМ-13
Студент: Дуркин Д. С.
Преподаватель: Цой Е. Б.
Новосибирск
2005
1 i). Найти методом
обратной функции моделирующее выражение для случайной величины ![]() , имеющей заданную плотность распределения
, имеющей заданную плотность распределения ![]()
Решение:
Постоянную ![]() найдем из условия
найдем из условия 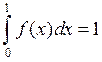 :
:
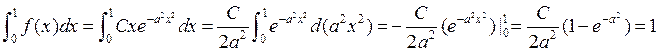 ,
,
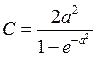 ,
, ![]() .
.
Плотность распределения случайной величины ![]() :
: 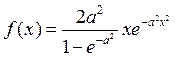
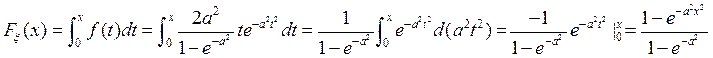
Моделирующее выражение:
![]()
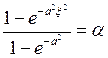 ,
,
![]() ,
,
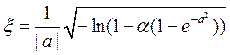 , где
, где
![]()
2 d).
Найти моделирующее выражение для случайной величины ![]() ,
имеющей плотность распределения
,
имеющей плотность распределения ![]() ,
,![]() , по методу обратной функции, когда
, по методу обратной функции, когда ![]() немонотонна.
немонотонна.
Решение:
Постоянную ![]() найдем из условия
найдем из условия 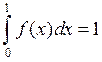 :
:
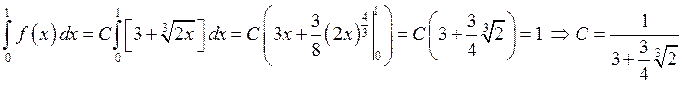
![]() ,
, ![]()
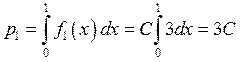
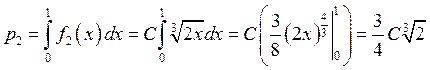
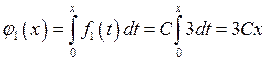
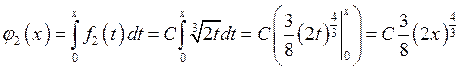
![]() ,
, 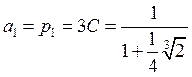 ,
, ![]()
Рассматриваем два случая:
1) 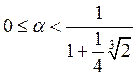
![]() ,
, 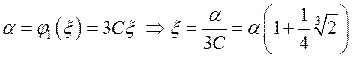 .
.
2) 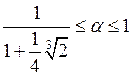
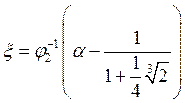 ,
, 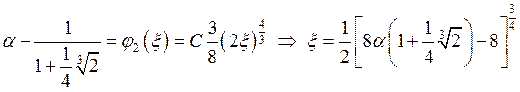
Таким образом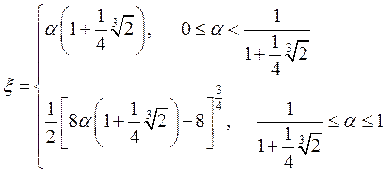 .
.
3 b).
Написать алгоритм моделирования случайной величины ![]() ,
распределённой по закону
,
распределённой по закону ![]() ,
, ![]() , с использованием порядковых статистик.
, с использованием порядковых статистик.
Решение:
Поскольку функция распределения ![]() имеет вид полинома Бернштейна при
имеет вид полинома Бернштейна при ![]() , то в этом случае коэффициент
, то в этом случае коэффициент ![]() и заданная плотность распределения
совпадает с плотностью распределения первой порядковой статистики для выборки
из четырех элементов, каждый из которых равномерно распределен на отрезке
и заданная плотность распределения
совпадает с плотностью распределения первой порядковой статистики для выборки
из четырех элементов, каждый из которых равномерно распределен на отрезке ![]() .
.
Таким образом алгоритм сводится к следующему:
Нужно сгенерировать случайные
величины ![]() и выбрать наименьшую из них.
и выбрать наименьшую из них.
4 b). Написать
алгоритм моделирования случайной величины ![]() ,
имеющей плотность распределения
,
имеющей плотность распределения 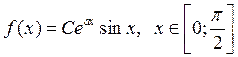 .
.
Решение:
Из условия нормировки функции
распределения определим константу ![]() :
:
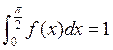 ,
,
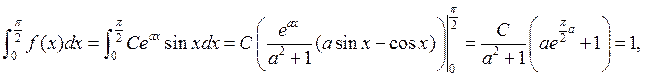
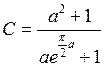 .
.
Тогда плотность функции
распределения имеет вид: 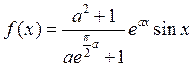 .
.
Поскольку видно, что метод обратной функции не дает решения через элементарные функции, то используем метод исключения.
Ограничим плотность
функции распределения ![]() сверху константой
сверху константой 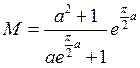 .
.
Алгоритм моделирования:
1) Генерируем два числа ![]()
2) Вычисляем 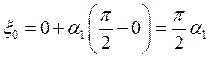 ,
, ![]() .
.
3) Если ![]() то
возвращаемся на шаг 1, иначе
то
возвращаемся на шаг 1, иначе ![]() [результат].
[результат].
5 c).
Написать алгоритм моделирования случайной величины ![]() с
плотностью распределения
с
плотностью распределения 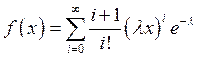 ,
, ![]() ,
, ![]() при
помощи метода суперпозиции.
при
помощи метода суперпозиции.
Решение:
Пусть 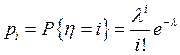 ,
,
![]() .
.
Тогда 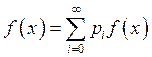 .
.
При этом ![]() ,
,
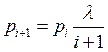 .
.
Алгоритм:
1) Генерируем ![]() .
.
2) Полагаем ![]() ,
, ![]() ,
, ![]() .
.
3) Вычисляем ![]() .
.
4) Если ![]() ,
то переходим на шаг 8, иначе на шаг 5.
,
то переходим на шаг 8, иначе на шаг 5.
5) Генерируем ![]()
6) Полагаем ![]() ,
, ![]() .
.
7) Если ![]() ,
то
,
то ![]() . Переходим на шаг 3.
. Переходим на шаг 3.
8) Полагаем ![]() [результат].
[результат].
6 f). Написать алгоритм
моделирования случайной величины ![]() с плотностью
распределения
с плотностью
распределения 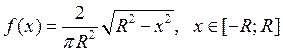 методом исключения.
методом исключения.
Решение:
Ограничим плотность функции
распределения ![]() сверху константой
сверху константой 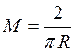 .
.
Алгоритм моделирования:
1) Генерируем два числа ![]()
2) Вычисляем ![]() ,
, ![]() .
.
3) Если ![]() то
возвращаемся на шаг 1, иначе
то
возвращаемся на шаг 1, иначе ![]() [результат].
[результат].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.