Метод магнитостатики конечных элементов на треугольниках

Министерство образования и науки РФ

НГТУ

Кафедра прикладной математики

Метод конечных элементов

Лабораторная работа №2

Факультет: ПМИ

Группа: ПМ-24

Студенты:

Бергинов А.В.

Воронов А.С.

Преподаватели:

Персова М.Г.

Задорожный А.Г

Новосибирск 2006 г.

Условие задачи.

Имеется двумерная область, с заданной конфигурацией материалов. Решить линейную и нелинейную задачу магнитостатики методом конечных элементов на треугольниках.

2.Математическая модель

Заданная область включает железный сердечник неправильной формы и две медные обмотки, расположенные внутри большого бака, заполненного воздухом. При постановке задачи магнитостатики материалы обладают следующими параметрами:

Задача магнитостатики в общем виде формулируется в следующим образом:

(1) 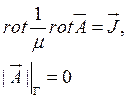      , где  - векторный потенциал поля,  - плотность тока,  - магнитная проницаемость.

(2)       .

В соответствии с этим решение также имеет только одну ненулевую компоненту:

(3)       .

Тогда уравнение (1) можно переписать в скалярном виде:

(4)       .

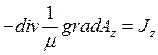Практическую ценность представляет собой не значение потенциала , а значение магнитной индукции . В соответствии с определением векторного потенциала:

(5)       .

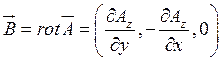В линейной задаче магнитная проницаемость железа постоянна для всего сердечника, в нелинейной задаче сердечник размагничивается и задается табличная зависимость .

Переходим к вариационной постановке задачи:

Решение задачи будем искать в Гильбертовом пространстве H¹ с введенным скалярным произведением и порождаемой им нормой.

Домножим уравнение скалярно на функцию v₀ H¹₀

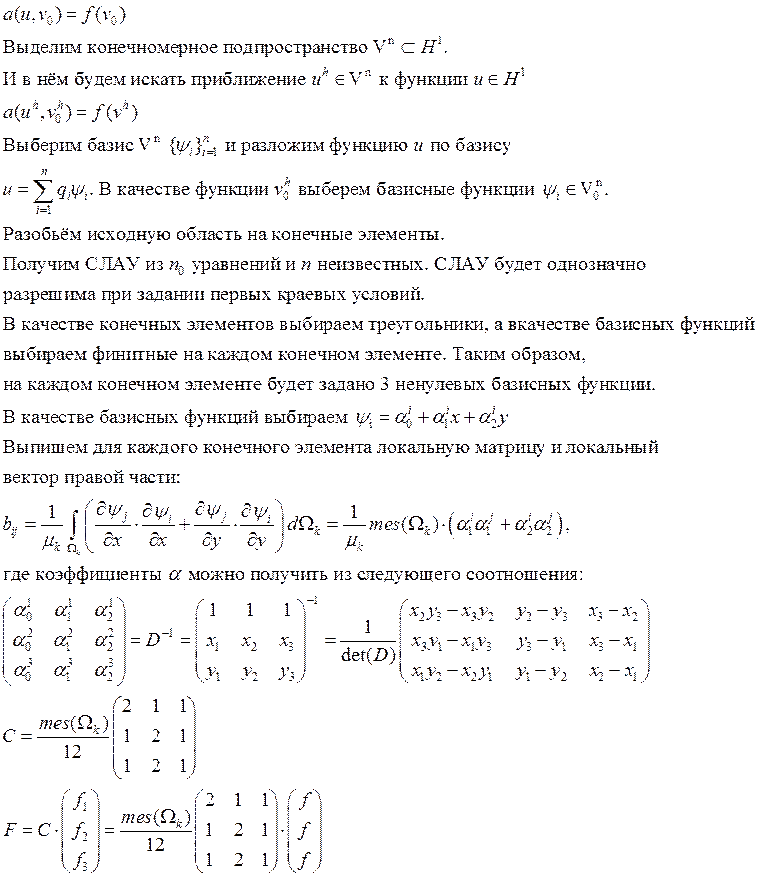
Методы решения задачи.

При решении линейной задачи в качестве решателя использовался метод ЛОС с предобуславливанием Холесского.

Нелинейная задача была решена методом простой итерации с использованием коэффициента релаксации.

Текст программы

Файл main.cpp

#include <conio.h>

#include <stdio.h>

#pragma hdrstop

#include "myclass.h"

void main()

{

clrscr();

field a;

SLAU my;

a.read_data();

my.formier_slau(a);

my.LOS();

my.x.print_vect("d:\\file\\res_my.txt");

printf("OK");

getch();

}

Файл const.h

#ifndef constH

#define constH

const char *FILE_XY="d:\\file\\xy.dat";

const char *FILE_INF2TR="d:\\file\\inf2tr.dat";

const char *FILE_NVTR="d:\\file\\nvtr.dat";

const char *FILE_MU="d:\\file\\mu";

const char *FILE_TOKU="d:\\file\\toku";

const char *FILE_KT1="d:\\file\\l1.dat";

const double MAX=1e60;

const double MAX_ITER=5000;

const double EPS=1e-15;

#endif

Файл myclass.h

//--------------------------------------------------------------------------#ifndef myclassH

#define myclassH

#include <math.h>

const long M=3;

//const double mu0=4.*M_PI*1e-7;

const double mu0=4.*M_PI*1e-7;

//

//--------------------------------------------------------------------------//структура - узлы сетки двумерной области

struct knot

{

double x;

double y;

};

//массив узлов сетки

struct mas_knot

{

knot *mas;

long n;

};

//-----------------------------------------------------//Локальная область

struct loc

{

long num_knot[3];//номера узлов в составе эл-та

long num_mat;//номер материала

};

//-----------------------------------------------------//массив локальных ообластей

struct mas_loc

{

loc *mas;

long n;

};

//------------------------------------------------------//Материал

struct mat

{

double toku;

double mu;

long num;

};

//------------------------------------------------------//Список материалов

struct mas_mat

{

mat *mas;

long n;

};

//1-е краевое

struct kt1

{

long num;

double a;

};

struct mas_kt1

{

kt1 *mas;

long n;

};

//------------------------------------------------------// Исходная область

class field

{

public:

mas_knot m_knot;// определяем узлы

mas_loc m_loc;// определяем локальные области

mas_mat m_mat;  // определяем список материалов

mas_kt1 m_kt1;

//можно сюда добавить краевые условия

void read_data();

double mes(long i);// Мера i-области (i=0..N-1)

double get_mu(long i);

double get_toku(long i);

};

//-------------------------------------------------------//список для эл-тов типа long

class list_long

{

public:

long el;

list_long *next;

list_long();

void add_el(long);

void del_el(long);

void free_list();

void print_list();

long get_ammount();

void copy_to_mas(long*);

};

//--------------------------------------------------------class VECTOR

{

public:

double *vect;

long n;

VECTOR();

VECTOR(long);

VECTOR(const VECTOR &a);

~VECTOR();

VECTOR operator=(VECTOR);

VECTOR operator+(VECTOR);

VECTOR operator-(VECTOR);

double operator*(VECTOR);

friend VECTOR operator*(double,VECTOR);