Метод Конечных Элементов. Решение двумерной гармонической задачи

Задание

Решить двумерную гармоническую задачу: 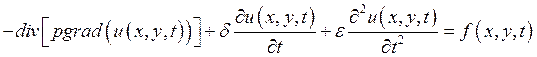, где .

Конечные элементы треугольные.

Базисные функции линейные.

Краевые условия первого рода.

Математическая модель

Решение поставленной задачи может быть найдено в ви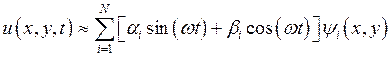де , где .

Помножим наше уравнение скалярно на пробную функцию и получим:

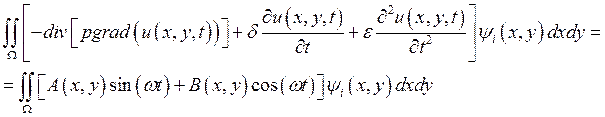, произведя разбиение расчетной области  на непересекающиеся подобласти , воспользуемся аддитивностью интеграла по области: 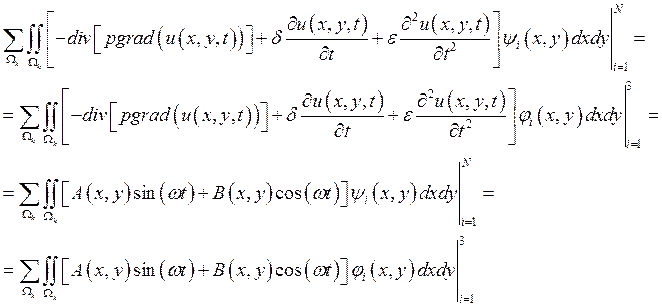 , таким образом, можно рассматривать вклад отдельных конечных элементов в i-тое уравнение системы.

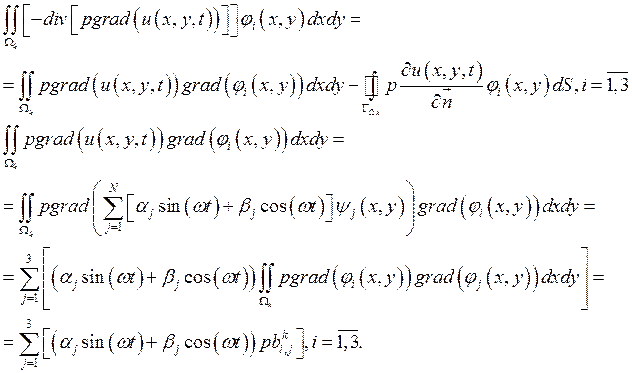
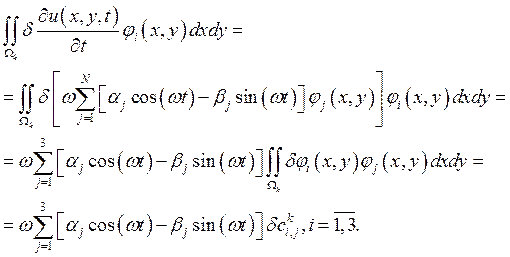
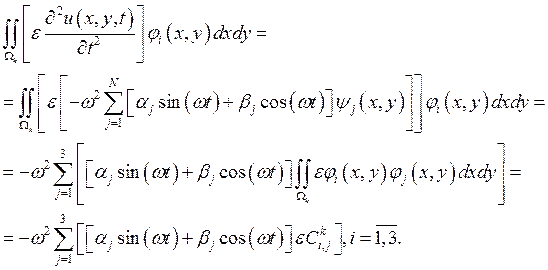
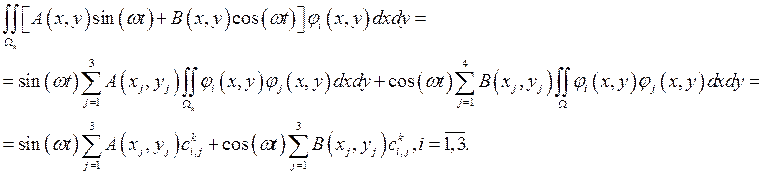 Таким образом получаем для каждого из конечных элементов следующий вклад в систему :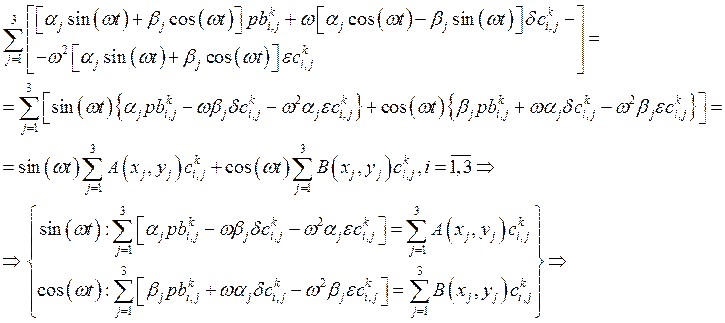

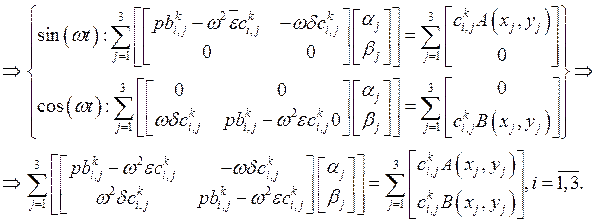
Вычислим  матрицы  и  для локальной матрицы на треугольниках, используя барицентрические координаты.

.

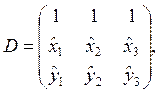
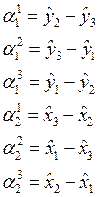
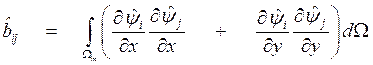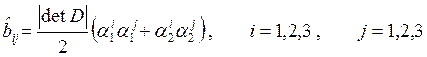
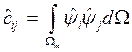
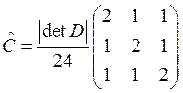
Тесты

Решение представляется в следующем виде:  для всех тестируемых функций использовались следующие параметры:

Сетка:

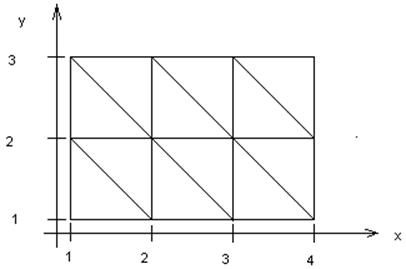
ü 

Относительная погрешность: 0.

ü 

Относительная погрешность: 0,009946

Относительная погрешность на раздробленной сетке: 0,005831

Отношение относительных погрешностей: 1,70571

ü 

Относительная погрешность: 0,005119

Относительная погрешность на раздробленной сетке: 0,001474

Отношение относительных погрешностей: 3,473005

Сетка:

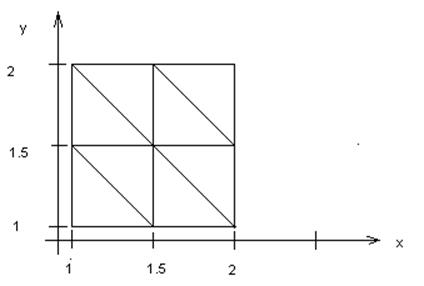
ü 

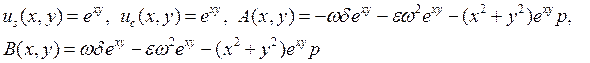
Шаг по сетке 0.5

Относительная погрешность: 4,11004E-05

Относительная погрешность на раздробленной сетке: 3,53183E-05

Отношение относительных погрешностей: 1,163713614

Шаг по сетке 0.1

Относительная погрешность: 1,17121E-10

Относительная погрешность на раздробленной сетке: 8,14949E-11

Отношение относительных погрешностей: 1,437161654

Шаг по сетке 0.01

Относительная погрешность: 9,55822E-19

Относительная погрешность на раздробленной сетке: 6,5632E-19

Отношение относительных погрешностей: 1,456335311

Выводы

v В ходе исследований выяснили, что на треугольных конечных элементах с линейными базисными функциями первый порядок аппроксимации.

v Преимущество данной задачи состоит в том, что решается стационарная задача, хотя размерность матрицы и увеличивается вдвое.