Метод конечных объемов

Новосибирский Государственный

Технический Университет

Курсовой проект

По дисциплине «Численные методы»

Факультет                      ПМ и И

Группа                             ПМ-72

Студентка                       Газизова НН

Преподаватель               Рояк МЭ  Соловейчик ЮГ

Новосибирск

1999

1.Постановка задачи

Решить методом конечных объемов эллиптическую краевую задачу на треугольных сетках, краевые условия 1-го,2-го и 3-го рода.

2.Введение

Метод конечных объемов заключается в том, что расчетная область разбивается на элементарные объемы, и дифференциальное уравнение заменяется на интегральные балансные соотношения для каждого из этих объемов. После этого интегралы в соотношениях аппроксимируются  с использованием значений искомой функции в узлах сетки или значений производных искомой функции, взятых из краевых условий.

Получим интегробалансные соотношения, на основании которых будет строиться дискретный аналог исходной краевой задачи. Для этого необходимо разбить расчетную область на конечные объемы и проинтегрировать по ним уравнение, причем конечные объемы должны быть построены таким образом, чтобы на их границах можно было вычислить потоки  с использованием значений искомой функции u в узлах сетки {x_k, y_k}.

Проинтегрируем дифференциальное уравнение по каждому из конечных объемов

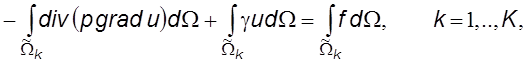
где K – общее число узлов в треугольной сетке. Применяя теорему Остроградского-Гаусса, преобразуем к виду

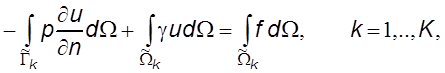
где  – граница конечного объема .

Расчетная область разбивается на треугольники. Внутри каждого треугольника функция u является линейной и может быть представлена, как линейная комбинация функций L₁(x, y), L₂(x, y) è L₃(x, y), каждая из которых равна 1 в одной из вершин треугольника и 0 в двух других. Через эти функции можно получить матрицу D, которая используется при вычислении вкладов в локальные матрицы.

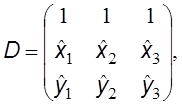
Используя эти функции, можно сравнительно легко получить вклады от данного треугольника в глобальную СЛАУ :

Значение компонент матрицы  могут быть получены из следующего соотношения:

 ,

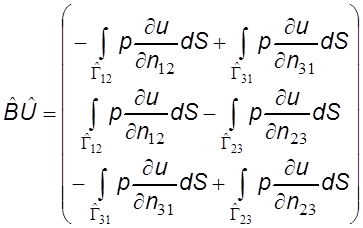Значения компонент матрицы  треугольника W_m могут быть получены из соотношения

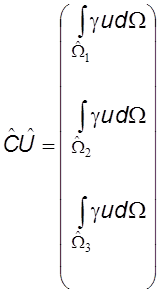
Значения компонент локального вектора  треугольника W_m могут быть получены из соотношения

.

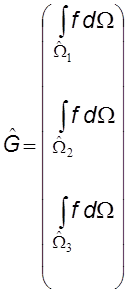для члена 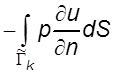 локальная матрица имеет вид :

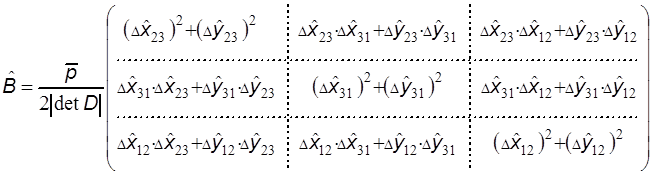
для члена — 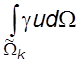 локальная матрица имеет вид:

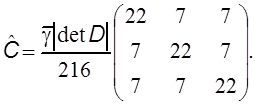                                                                                                  где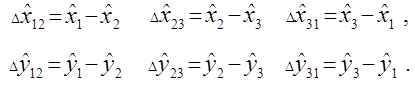

1,2 и 3 — локальные номера вершин треугольника.

В каждом треугольнике содержатся вклады в конечные объемы, построенные вокруг вершин треугольника.

Глобальная матрица составляется из локальных матриц путем занесения в m-ю строку глобальной матрицы строки, соответствующей вершине треугольника с глобальным номером m.

3.Алгоритм решения 

Решение задачи удобнее всего разбить на части:

·  Составление глобальной матрицы

·   составление локальных матриц для каждого треугольника

·  Учет краевых условий

·  учет 3-х краевых условий

·  учет 2-х краевых условий

·  учет 1-х краевых условий

Все части организованы, как подпрограммы.

Информация об условиях задачи хранится в файлах

·  xy.dat  — массив узлов сетки

·  nvtr.dat — описание треугольников (номера вершин и тип материала)

·  l1.dat — номера узлов, в которых заданы 1-е краевые условия

·  l2.dat — ребра, в которых заданы 2-е краевые условия (номера вершин ребер)

·  l3.dat — ребра, в которых заданы 3-и краевые условия

В программе хранятся координаты вершин и глобальная матрица.

3.Тестирование

·  -div(grad u)  = 0, при  х=0 u=0, при х=5 u=5

    

                                                Так задана сетка для этой задачи                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                  

Глобальная СЛАУ для этой задачи имеет вид

2.91666675     -2.5      0          | 1.25

-2.5      5.83333349     -2.5      | 2.5

0          -2.5      2.91666651     | 1.25      

Значения искомой функции в узлах

u1=0    u2=3.00000025           u3=5

u4=0    u5=3.00000047           u6=5

u7=0    u8=2.99999953           u9=5

·  -div(grad u) = 0                 при x=0 u=y, при x=2 u`|y=1

при y=0 u=x, при y=2 u`|x=1

 

Так задана сетка для этой задачи              

Глобальная СЛАУ имеет вид

4          -1         -1         0          |           2

-1         2          0          -0.5      |           2

-1         0          2          -0.5      |           2

0          -0.5      -0.5      1          |           1

Значения искомой функции в узлах сетки

u1=0    u2=1    u3=2

u4=1    u5=2    u6=3

u7=2    u8=3    u9=4