Метод бисопряженных градиентов. Метод бисопряженных градиентов стабилизированный

1.1.1. Метод бисопряженных градиентов

Стандартный метод бисопряженных градиентов (BCG), предложенный К. Ланцошем [3] в 1952 г. (дальнейшее развитие метод получил в книгах Д.К. и В.Н. Фаддеевых [111] и Р. Флетчера [2]), применим для произвольных невырожденных систем уравнений [44].

Алгоритм BCG [44] для системы уравнений  выглядит следующим образом.

Выбирается начальное приближение  и полагается

                                                                                                .                                       

Выбирается ненулевой вектор  и полагается . Далее для  производятся следующие вычисления:

,                                                                                  ,                                                                                  ,                                                                                ,                                                                                  ,                                                                                        ,                                                                                       .                                

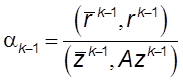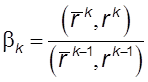Если  или , процесс заканчивается.

Применим алгоритм BCG для предобусловленной системы уравнений , для этого в формулах - введем новые величины с символами .

Выбирается начальное приближение  и полагается

                                                                    ,                                                          .                                   

Далее для  производятся следующие вычисления:

,                                                                       ,                                                                       ,                                                                     ,                                                                             ,                                                                                      ,                                                                                      .                                

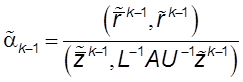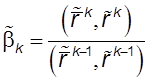Отметим, что вместо формул удобнее использовать формулу

,                           тогда на каждой итерации решения СЛАУ мы будем иметь значение вектора , являющегося решением исходной (не предобусловленной) системы уравнений.

Учитывая и вводя, с целью минимизации вычислительных затрат, новые векторы

,     ,     ,     , получим вместо схемы - схему метода бисопряженных градиентов с предобусловливанием в виде неполной факторизации.

Выбирается начальное приближение  и полагается

                                                                                                        ,                                                .                                    

Далее для  производятся следующие вычисления:

,                                                                    ,                                                                     ,                                             ,                                                  ,                                                                          ,                                                                                        .                                      

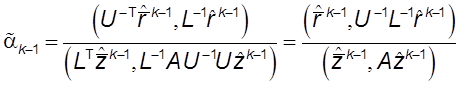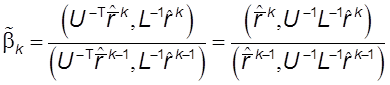Процесс заканчивается если величина  – квадрат нормы невязки стала достаточно малой.

Отметим, что дополнительные (сверх затрат памяти на СЛАУ) затраты памяти на реализацию метода сопряженных градиентов с предобусловливанием в виде неполной факторизации составляют 5 вещественных векторов, размерности , где – размерность СЛАУ. Это рекуррентно вычисляемые векторы , , ,  и один вспомогательный вектор. Размерность векторов равна размерности СЛАУ.

1.1.2. Метод бисопряженных градиентов стабилизированный

Алгоритм Bi-CGStab [15, 44] для системы уравнений  выглядит следующим образом:

Выбирается начальное приближение  и полагается

                                                                                                .                                       

Далее для  производятся следующие вычисления:

,                                                                                 ,                                                                                          ,                                                                                     ,                                                                          ,                                                                                     ,                                                                            .                    

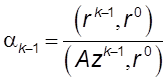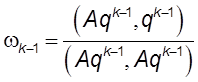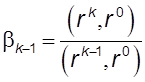Применим алгоритм Bi-CGStab для предобусловленной системы уравнений , для этого в формулах - введем новые величины с символами .

Выбирается начальное приближение  и полагается

                                                                                          ,                                                              .                                       

Далее для  производятся следующие вычисления:

,                                                                       ,                                                                           ,                                                                          ,                                                                     ,                                                                               ,                                                                      .               

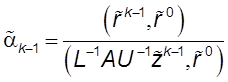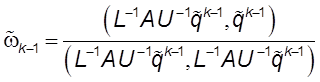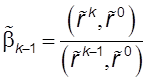После окончания итерационного процесса необходимо вычислить решение исходной СЛАУ по формуле

.                                     

Отметим, что дополнительные (сверх затрат памяти на СЛАУ) затраты памяти на реализацию метода бисопряженных градиентов стабилизированного с предобусловливанием в виде неполной факторизации составляют 5 вещественных векторов, размерности , где – размерность СЛАУ. Это рекуррентно вычисляемые векторы , ,  вектор  и один вспомогательный вектор. Размерность векторов равна размерности СЛАУ.