Машинная имитация.Методология машинной имитации.Математические модели сложных систем. Типы математических моделей.

Вычисление –lna можно заменить моделированием показательного распределения.

Лекция 12      

Общая схема метода Монте-Карло. Роль закона больших чисел и предельных теорем в теории статистического моделирования. Статистическая теория оценивания.

1.

Возможность моделирования случайных величин и процессов может быть использована  для моделирования реальных явлений и ситуаций. При этом наблюдение небольшого числа реализаций случайной величины вряд ли принесет пользу, но наблюдение на большем их числом позволят сделать правильные выводы об их средних характеристиках.

Такой подход лежит в основе метода Монте-Карло, который использует различные придельные соотношения теории вероятностей.

-  закон больших чисел              

-  придельные теоремы

Пример:       Предложить схему вычисления числа p .

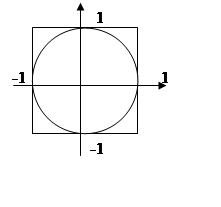
p=S_O/S   -  вероятность попадания в круг.

S =4

S_O=pr²=p                   

p=p/4

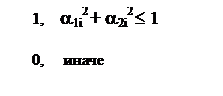
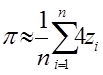                Z_i    = 

2.

Теорема  ( А. Колмогоров )

Для того, что бы среднее арифметическое независимых реализаций случайной велечины x сходилось с вероятностью 1 к ее математическому ожиданию, необходимо и достаточно, чтобы это математическое ожидание существовало.

Эта теорема, - усиленный закон больших чисел в форме А. Колмогорова и состовляет принципиальную основу использования метода Монте-Карло для вычисления математического ожидания случ. велечины на основе ее независимых реализаций.

Пусть x - произвольная случайная велечина, М[x]=m

x₁ , x₂ … x_n  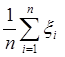,           =   ,     ,  при

Рассмотрим примеры, где можно использовать вышеприведенные вычислительные схемы.

Пример 1

Пусть требуется выполнить расчет надежности изделия, состоящего из значительного числа элементов, для которых в результате эксперемента удалось построить распределение времени безотказной работы.

Если это время распределено по показательному закону для всех элементов, то задачу удастся решить аналитически. Если же имеют место отказы в результате износа элементов распределенные по нормальному закону или усеченному нормальному закону, то аналитическое решение невозможно.

Пусть изделие работоспособное, если работоспособны элементы, состовляющие одну из цепочек 1-7.

 

1

7

3

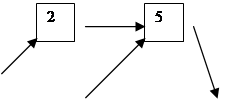начало                                                                             конец

 

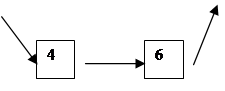Пусть t_i –случайная велечина, равная времени безотказной работы элемента i

Тогда среднее время безотказной работы можно представить как математическое ожидание x, где

x =min{t₁;max[min(t₄,t₆);min(max(t₂,t₃),t₅)];t₇}.

Итак, закон больших чисел обеспечивает сходимость 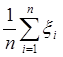  к  М[x].

Пример 2       Численное решение задачи Сильвестра.

Пусть задана выпуклая область D на плоскости и функция совместного распределения G( x₁, y₁, …, x_r,y_r ) четырех точек А_i=( x_i , y_i )ÎD. Найти вероятность того, что случайные точки образует выпуклый четырехугольник.

                               .

.   .             .      .                   

       .

   .                     .

1,  если полученный четырехугольник выпуклый

Пусть x=

0, невыпуклый              

Очевидно, что 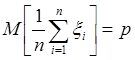  - искомая вероятность.

Для зависимых случайных велечин  также имеют место законы больших чисел.

Пусть g₁ , g₂ , …, последовательность случайных состояний стационарной цепи Маркова с переходной матрицей P.

Теорема  ( Усиленный закон больших чисел для цепи Маркова ).

Если p^T=|| p₁, p₂, …, p_n || - единственное стационарное распределение стохастической матрицы P, то  для любого начального распределения p₀ и произвольной функции состояний f(g) имеет место равенство:

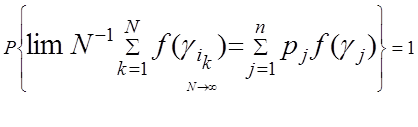
где  i₁®i₂®… - последовательность переходов цепи Маркова.

Теорема  ( Закон больших чисел в ослабленной форме ).

Для того, чтобы для последовательности x₁ , x₂ …- случайных велечин таких, что существует и конечно M[x_i] ( при произвольном характере их зависимости)

" e>0 выполнялось соотношение :

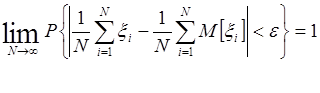  необходимо и достаточно, чтобы выполнялось равенство:

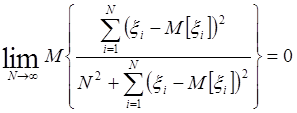
3.

Итак законы больших чисел, хотя и могут служить принципиальным обоснованием методов стат. моделирования, но они не позволяют судить об их погрешности. Поведение погрешности можно изучить, используя

предельные теоремы теории вероятности.

Будем различать 4 основные задачи.

             А                         Б                               В                           Г

x_i – независимые       x_i – независимые        x_i – зависимые       x_i – зависимые

М[x²] –известные      М[x²] –известные   М[x²] –известные   М[x²] -известные конечные                    конечные                 конечные                конечные

М[x] - ?  - задача вычисления математич. ожидания случайной велечины x.

В случае А для изучения поведения погрешности используется классическая предельная теорема.

Пусть  x₁ , x₂ , …, - независимые случайные велечины, существуют и конечны: m_k=M[x_k] , d²_к=D[x_k]. Пусть L²_к=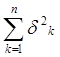

Теорема

Если последовательность x₁ , x₂ , …, при любом постоянном t > 0 удовлетворяет  условию Линдеберга

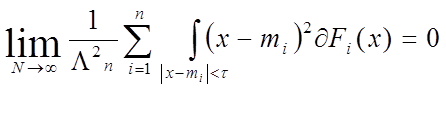,              (1)

где  F_i(x) - функция распределения x_i ,то при  n®µ равномерно относительно x

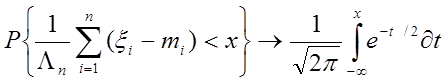                (2)

Эта теорема сформулирована без предположения об одинаковой распределенности x_i.  При наличии его, условие (1) вытекает из конечности второго момента