Математическое обеспечение.Множественная регрессия

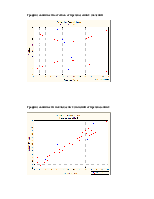
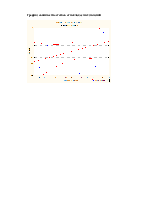
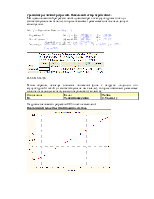
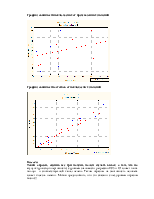
Испытуемыми были студенты мужского пола, возраст 20-22 года, Санкт-Петербургского государственного технического университета. У каждого из них проводилось измерение электрокожного сопротивления в 24 биологически активных точках (12 слева и 12 справа), являющихся проекциями отдельных органов. Результаты приведены в таблице 1.

Таблица 1. Наименование и обозначение репрезентативных точек

Таблица 2. Диагностируемые психологические свойства

Математическая постановка задачи

Модель множественной регрессии 1

Введем используемые далее обозначения: уравнение регрессии имеет вид         Z_i = b₀+b₁*X_i + e_{i   ,} i=1…12 , где e_i есть независимые случайные ошибки со средним 0, которые интерпретируются как ошибки наблюдений,  — неизвестные параметры,  которые следует оценить по наблюдениям.

Зависимая переменная Z1 - акцентуация.  В качестве факторных переменных используются  переменные Xi – фоновые значения электрокожного сопротивления;

Оценки параметров  обозначаются как .

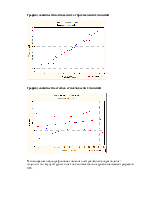
Выполним регрессионный анализ

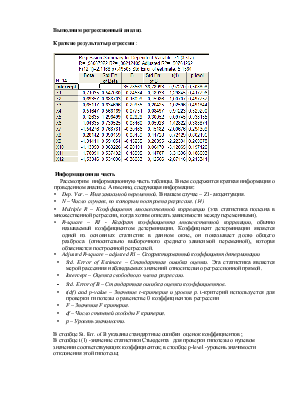
Краткие результаты регрессии :

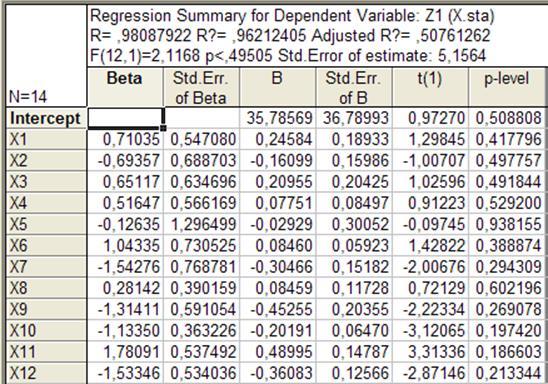
Информационнаячасть

Рассмотрим  информационную часть таблицы. В нем содержится краткая информация о проведенном анализе. А именно, следующая информация:

•  Dep. Var. – Имя зависимой переменной. В нашем случае – Z1- акцентуация.

•  N– Число случаев, по которым построена регрессия. (14)

•  MultipleR– Коэффициент множественной корреляции (эта статистика полезна в множественной регрессии, когда хотим описать зависимости между переменными).

•  R-square– RI - Квадрат коэффициента множественной корреляции, обычно называемый коэффициентом детерминации. Коэффициент детерминации является одной из основных статистик в данном окне, он показывает долю общего разброса (относительно выборочного среднего зависимой переменной), которая объясняется построенной регрессией.

•  AdjustedR-square – adjustedR1 – Скорректированный коэффициент детерминации

•  Std. Error of Estimate – Стандартнаяошибкаоценки. Эта статистика является мерой рассеяния наблюдаемых значений относительно регрессионной прямой.

•  Intercept–Оценка свободного члена регрессии.

•  Std. ErrorofB –Стандартная ошибка оценки коэффициентов.

•  t(df) andp-value–Значение t-критерия и уровня р. t-критерий используется для проверки гипотезы о равенстве 0 коэффициентоврегрессии

•  F – Значения F критерия.

•  df–Число степеней свободы F критерия.

•  р –Уровень значимости.

В столбце St. Err. of B указаны стандартные ошибки  оценок коэффициентов ;

В столбце t(1) -значение статистики Стьюдента   для проверки гипотезы о нулевом значении соответствующих коэффициентов; в столбце p-level -уровень значимости отклонения этой гипотезы;

Если R² = 0, это означает, что регрессия ничего не дает, т.е. знание х не улучшает предсказания для y по сравнению с тривиальным. Другой крайний случай R² = 1 означает точную подгонку: все точки наблюдений лежат на регрессионной прямой. Чем ближе к 1 значение R² , тем лучше качество подгонки

В нашем случае значение коэффициента детерминации R² =0,96 , то есть регрессия объясняет 96% разброса значений Z относительно среднего.

Проверка гипотезы о нулевых значениях коэффициентов регрессии. Для проверки гипотезы Н₀ об отсутствии какой бы то ни было линейной связи между y и совокупностью факторов, Н₀: b₁ = b₂ = ... = b_k = 0, т.е. об одновременном равенстве нулю всех коэффициентов, кроме коэффициента b₀    при константе, используется статистика

F = 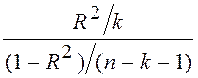 =  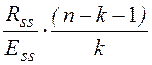=  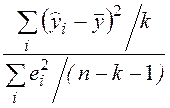,      распределенная, если Н₀ верна, по закону Фишера с k и n - k - 1 степенями свободы. Н₀  отклоняется, если           F > F_a (k, n - k - 1),     где F_a - квантиль уровня 1 - a.

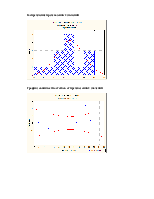
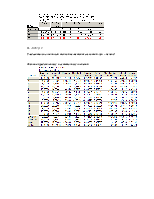
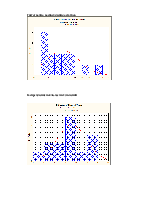
В то же время проверка гипотезы об отсутствии какой бы то ни было линейной связи между Z и (х₁ , ..., х₁₂)  , где F(12,1)=2,12 p=0,5  отклоняется т.к  F < F_a (k, n - k - 1)=60.7, где  _{a =0.05 ,}k=12 , n=14   говорит о том, что следует продолжить изучение линейной связи между y и  (х₁ , ..., х₁₂), анализируя как их содержательный смысл, так и матрицу парных корреляций, которая определяется так:

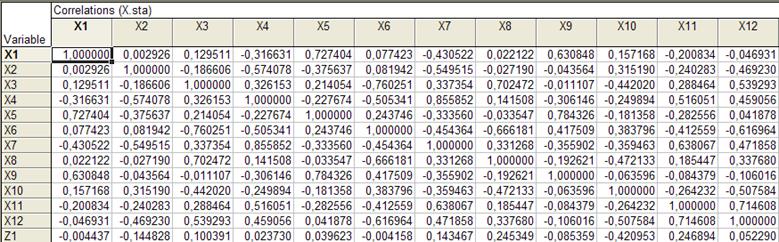
Из матрицы видно, что некоторые пары коррелированны, таким образом имеет место дублирование информации, и по-видимому, есть возможность перехода от исходного числа переменных к меньшему.

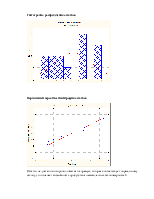
Сравнение различных регрессий. Пошаговый отбор переменных.

Методами пошаговой регрессии необходимо выбрать те акупунктурные точки (и соответствующие им каналы), которые оказывают решающее влияние на заданную акцентуацию

Forward stepwise

Multiple Regression Results (Step   1)

Dependent: Z1               Multiple R =  ,42095346     F = 2,584378

R?=  ,17720182    df =   1,12

No. of cases: 14            adjusted R?=  ,10863530     p =  ,133900

Standard error of estimate: 6,937845027

Intercept: 19,846364684  Std.Error: 5,221137  t(   12) = 3,8012  p =  ,0025

X10 beta=-,42

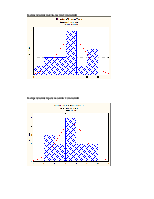
Backward stepwise

Multiple Regression Results (Step  12)

Dependent: Z1               Multiple R = 0.00000000     F = 0.000000

R?= 0.00000000    df =   0,13

No. of cases: 14            adjusted R?= 0.00000000     p = -0.00000

Standard error of estimate: 7.348469228

All variables have been removed from the regression equation