Министерство образования и науки Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра прикладной математики и информатики
Группа: ПМ-15
Студенты: Голубева М. В.
Кичаева Н. А.
Вариант: 2
Преподаватели: Пономаренко В.М.
Ванюкевич О.Н.
Новосибирск
2005
1. Цель работы:
Изучение основных способов представления математических проблем в символьном виде, пригодном для формальной обработки на компьютере.
2. Задание
1. На примере программы символьного дифференцирования, прилагаемого к данной лабораторной работе, рассмотреть структуру данных для представления математических выражений.
2. Развить данную структуру для представления вещественных чисел, комплексных чисел.
3. Познакомиться с принципами лексического и синтаксического анализа входных строковых выражений, представляющих математические тексты.
4. Познакомиться с принципами трансляции из внутреннего представления математических выражений во внешнее – строковое.
5. Рассмотреть Пролог – программу для символьного дифференцирования и упрощения алгебраических выражений с точки зрения декларативной семантики (как систему аксиом)
6. Используя в качестве прототипа программу аналитического дифференцирования, составить программу аналитического интегрирования для выбранного класса функций.
3. Реализация
1. Для того чтобы можно было использовать вещественные числа при работе с программой были внесены следующие изменения (с учетом того, что множество вещественных чисел включает в себя множество целых):
В определении типа EXP заменили int(INTEGER) на int(REAL).
Далее при разборе строк используется функция конвертации строки в переменную типа int, эту функцию везде заменим на функцию конвертации строки в переменную типа real:
В разделе “CLAUSES FOR CONVERTING AN EXPRESSION TO A STRING”:
strexp(int(INT),INTSTR) :- str_int(INTSTR,INT).
В разделе “CLAUSES FOR PARSING OF AN EXPRESSION”:
elmexp(["-",TALSTR|IL],IL,int(INT)):-
str_int(TALSTR,INTp),
INT = -INTp.
INT = -INTp.
elmexp([TALSTR|IL],IL,int(INT)):-str_int(TALSTR,INT),!.
2. Для использования функции “экспонента” были введены следующие правила:
a) При разборе строки в разделе CLAUSES FOR PARSING OF AN EXPRESSION
elmexp(["exp","("|IL],OL,exp(EXP)):-
s_exp(IL,OL1,EXP),
front(")",OL1,OL),!.
b) При конвертации выражения в строку в разделе CLAUSES FOR CONVERTING AN EXPRESSION TO A STRING
strexp(exp(EXP),STR) :-
strPAR(EXP,STRp),
concat("exp",STRp,STR).
3. Далее что касается аналитического интегрирования сначала, сформулируем свойства интегралов использованные для данной программы:
1) ![]() , а = const
, а = const
2) ![]()
3) 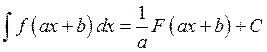
4) 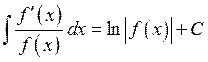
5) ![]()
Для реализации этих свойств был введен предикат i(EXP,EXP,EXP), означающий что
i(U,X,V) Þ ![]() .
.
Также были реализованы основные табличные интегралы.
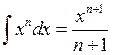 ,
, ![]()
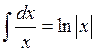 ,
, ![]()
![]()
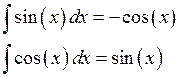
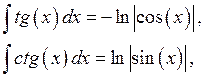
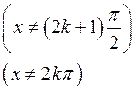
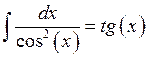 ,
, 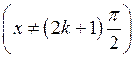
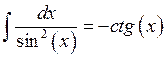 ,
, ![]()
Для реализации свойств интегралов введены следующие правила:
i(int(0),_,int(0)):-!.
i(int(Y),X,mult(int(Y),var(X))):-!.
i(var(Y),X,mult(var(Y),var(X))):-!.
Для реализации свойства 2. аддитивности.
i(plus(U,V),X,plus(U1,V1)):i(U,X,U1),
i(V,X,V1).
i(minus(U,V),X,minus(U1,V1)):i(U,X,U1),
i(V,X,V1).
Для реализации умножения на число.
i(mult(int(Y),V),X,mult(int(Y),V1)):i(V,X,V1),!.
i(mult(V,int(Y)),X,mult(int(Y),V1)):i(V,X,V1),!.
Для реализации интегрирования по частям.
i(mult(U,DV),X,minus(mult(U,V),I)) :-
d(U,X,DU),
i(DV,X,V),
reduce(mult(DU,V),M),
i(M,X,I), !.
Для реализации свойства 4.
i(div(DU,U),X,ln(U)):d(U,X,H),
reduce(H,DU),!.
i(div(int(A),U),X,mult(div(ln(U),I),int(A))) :d(U,X,I),!.
Степенная функция.
i(potens(E1,int(I)),_,div(potens(E1,int(I1)),int(I1))):-
I1=I+1.
Экспонента.
i(exp(U),X,div(exp(U),I)):-d(U,X,I),!.
Логарифмическая функция.
i(ln(var(X)),X,minus(mult(var(X),ln(var(X))),var(X))).
Тригонометрические функции.
i(sin(Y),X,div(mult(int(-1),cos(Y)),V)):d(Y,X,V),!.
i(cos(Y),X,div(sin(Y),V)):-d(Y,X,V).
i(tan(U),X,mult(int(-1),ln(cos(U1)))):-d(U,X,U1),!.
i(div(int(1),tan(U)),_,DU):-reduce(mult(int(1),ln(sin(U))),DU),!.
i(div(int(1),potens(sin(U),int(2))),X,div(mult(int(-1),div(int(1),tan(U))),H)):d(U,X,H),!.
i(div(int(1),mult(sin(U),sin(U))),X,div(mult(int(-1),div(int(1),tan(U))),H)):d(U,X,H),!.
i(div(int(1),potens(cos(U),int(2))),X,div(mult(int(1),tan(U)),H)):d(U,X,H),!.
i(div(int(1),mult(cos(U),cos(U))),X,div(mult(int(1),tan(U)),H)):d(U,X,H),!.
4. Тестирование программы
|
Исходная функция - f(x) |
Значение интеграла - F(x)+C |
|
0.9999 |
0.9999*x+C |
|
2.3*x |
2.3*x^2+C |
|
7.1/x |
7.1*ln(x)+C |
|
2.0*sin(9*x)-x^2 |
2*-1*cos(9*x)/9-x^3/3+C |
|
9.2/(9.2*x) |
ln(9.2*x)+C |
|
s+0.9*tan(1.2*x) |
s*x+-0.75*ln(cos(1.2*x))+C |
|
2.0/tan(9.0*x) |
2*ln(sin(9*x))/9+C |
|
2.0*exp(0.9*x) |
2*exp(0.9*x)/0.9+C |
|
8/cos(9*x)^2+5/(sin(2*x)*sin(2*x)) |
8*tan(9*x)/9+-1*5/tan(2*x)/2+C |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.