
















ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №1,2.
Тема: Комплексные числа и действия над ними.
Комплексными
числами (к.ч.) называются пары (![]() ) действительных чисел
) действительных чисел ![]() и
и ![]() , если
для них определены понятия равенства и операции сложения и умножения следующим
образом:
, если
для них определены понятия равенства и операции сложения и умножения следующим
образом:
1. Два к.ч. (![]() ) и (
) и (![]() ) равны
) равны ![]()
![]() ,
, ![]() .
.
2. Суммой двух к.ч. (![]() ) и (
) и (![]() )
называется к.ч. (
)
называется к.ч. (![]() ) .
) .
3.
Произведением к.ч. (![]() ) и (
) и (![]() )
называется к.ч. (
)
называется к.ч. (![]() )
)
Каждое к.ч. (![]() ) принято обозначать символом
) принято обозначать символом ![]() и оно представимо в алгебраической
форме:
и оно представимо в алгебраической
форме: ![]() . Число
. Число ![]() называется
действительной частью к.ч.
называется
действительной частью к.ч. ![]() , обозначается Re
, обозначается Re![]() ; число
; число ![]() называется
мнимой частью к.ч.
называется
мнимой частью к.ч. ![]() , обозначается символом
, обозначается символом ![]() .
.
Величина ![]() называется модулем к.ч.
называется модулем к.ч. ![]() , обозначается символом
, обозначается символом ![]() :
: ![]() =
=![]() .
.
Любое число ![]() , удовлетворяющее равенствам
, удовлетворяющее равенствам 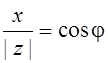 ,
, 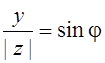 ,
называется аргументом к.ч.
,
называется аргументом к.ч. ![]() , обозначается символом
, обозначается символом ![]() . Аргумент определен для z¹0 лишь с
точностью до любого слагаемого, кратного 2p,
то есть j=argz+2kp, kÎZ. Для
однозначных функций
. Аргумент определен для z¹0 лишь с
точностью до любого слагаемого, кратного 2p,
то есть j=argz+2kp, kÎZ. Для
однозначных функций 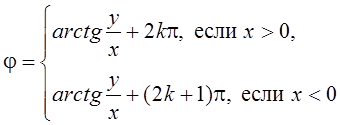 , kÎZ и arctg
, kÎZ и arctg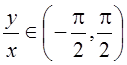 .
.
Тригонометрической
формой к.ч.![]() называется его запись в виде
называется его запись в виде ![]() .
.
В показательной
форме к.ч. ![]() имеет вид
имеет вид ![]() или
или ![]() , где
, где ![]() =
=![]() (формула Эйлера).
(формула Эйлера).
К. ч. ![]() называется сопряженным с к.ч.
называется сопряженным с к.ч. ![]() , обозначается символом
, обозначается символом ![]() :
: ![]() , если
, если ![]() .
.
Ответить на вопросы.
1. Перечислить свойства операций сложения и умножения к.ч.
2. Определить операции вычитания и деления на множестве к.ч.
3. Определить операцию извлечения корня степени n, n- целое, на множестве комплексных чисел.
4. Записать число x+iy как результат действия над парами.
5. Показать, что i2= -1.
6. Показать, что множество действительных чисел может быть рассмотрено как подмножество комплексных чисел.
7. Дать геометрическую интерпретацию комплексных чисел.
Практическая часть.
1. Выполнить действия:
1. ![]() ; 2.
; 2. 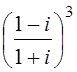 ; 3.
; 3. 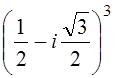 ; 4.
; 4. 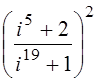 ; 5.
; 5.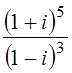 .
.
2. Найти модули и аргументы комплексных чисел
1.![]() ;
;
2. -3;
3.1+![]() ;
;
4.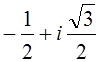 ;
;
5.![]() ;
;
6.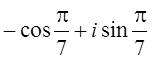 ;
;
7.![]() ;
;
8.![]() ;
;
9.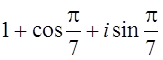 .
.
3. Доказать равенства:
1.![]() ;
;
2.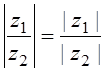 ;
;
3.![]()
![]() ;
;
4.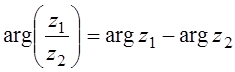
![]() ;
;
5.![]()
6.![]() ;
;
7.![]() ;
;
8.![]() ;
;
9.![]() ;
;
Примечание.![]()
4. Дать геометрическое описание множеств всех точек комплексной плоскости, удовлетворяющих следующим соотношениям:
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
5. ![]()
6. ![]() ;
;
7. ![]() ;
;
8. ![]() ;
;
9. 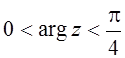 ;
;
10. 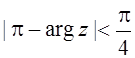 ;
;
11. ![]() ;
;
12. ![]() ;
;
13. ![]() ,
, 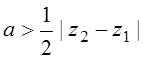 ;
;
14. ![]() ;
;
15. 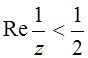 ;
;
16. 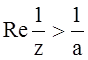 , a>0;
, a>0;
17. 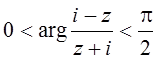 ;
;
18. 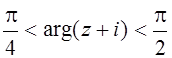 ;
;
19. ![]() ;
;
20. ![]() .
.
5. Какие линии записаны уравнениями:
1. 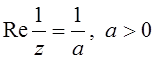 ; 2.
; 2.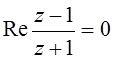 ; 3.
; 3.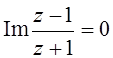 ; 4.
; 4.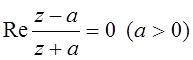 .
.
6. Найти все решения систем уравнений:
1.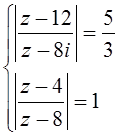 2.
2. 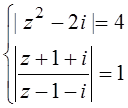
7. Записать с помощью неравенств следующие множества комплексной плоскости:
1. Полуплоскость, расположенная справа от мнимой оси.
2. Первый квадрант.
3. Полуплоскость, расположенная выше действительной оси и состоящая из точек, отстоящих от действительной оси на расстояние, не меньшее 2.
4. Полоса, состоящая из точек, отстоящих от мнимой оси на расстояние, меньшее 1.
5. Полукруг радиуса 1 (без
окружности) с центром в точке ![]() , расположенный слева от
мнимой оси.
, расположенный слева от
мнимой оси.
8. Найти геометрический смысл следующих величин:
1.![]() ; 2.
; 2.![]() ; 3.
; 3.![]() ;
;
9. Доказать равенства
1. ![]() ; 2.
; 2. ![]() ,
, ![]() ; 3.
; 3. 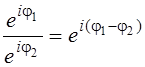 .
.
10. Вывести формулы: 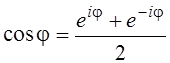 ,
, 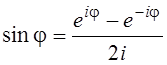 .
.
11. Вычислить суммы:
1. ![]() ,
, ![]()
2. ![]() ,
, ![]()
3. ![]() ,
, ![]()
4. ![]() ,
, ![]()
5. ![]()
![]()
6. ![]()
12. Найти все решения уравнений:
1. ![]() ;
;
2. ![]() ;
;
3. ![]() = -1;
= -1;
4. ![]() =64;
=64;
5. ![]() +1=0;
+1=0;
6. ![]() ;
;
7. ![]() ;
;
8. ![]() .
.
13. Пусть ![]() -произвольный корень
степени
-произвольный корень
степени ![]() из единицы, отличный от единицы. Доказать:
из единицы, отличный от единицы. Доказать:
1. 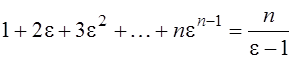 ;
;
2. 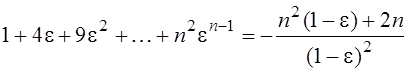 ;
;
Ответы и указания.
1. 1. ![]() ; 2.
; 2. ![]() ; 3. -1;
4.
; 3. -1;
4. 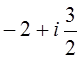 ; 5. 2.
; 5. 2.
2. 1.![]() =1,
=1, 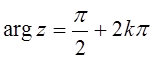 ,
, ![]() ;
;
2. ![]() ,
, ![]() ,
, ![]() ;
;
3. ![]() ,
, 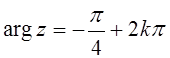 ,
, ![]() ;
;
4. ![]() ,
, 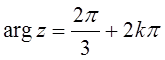 ,
, ![]() ;
;
5. ![]() ,
, 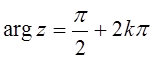 ,
, ![]() ;
;
6. ![]() ,
, 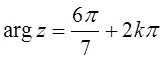 ,
, ![]() ;
;
7. ![]() ,
, 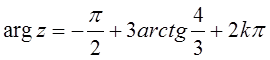 ,
, ![]() ;
;
8. 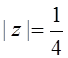 ,
, ![]() ,
, ![]() ;
;
9.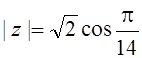 ,
, 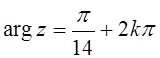 ,
, ![]() ;
;
3. Воспользоваться определением модуля и аргумента комплексных чисел.
4. 1. Полуплоскость, расположенная справа от мнимой оси (точки оси не включаются);
2. Полуплоскость, расположенная
ниже горизонтальной прямой, проходящей через точку ![]() (точки
прямой включаются);
(точки
прямой включаются);
3. Полоса, состоящая из точек, расстояние от которых до мнимой оси меньше 1;
4. Прямоугольник с вершинами в
точках ![]() ,
, ![]() ,
, ![]() ,
, ![]() (стороны
не включаются);
(стороны
не включаются);
5. Круг радиуса 1 с центром в
точке ![]() (включая окружность);
(включая окружность);
6. Вся плоскость, из которой
удален круг радиуса 1 с центром в точке ![]() вместе
с его окружностью;
вместе
с его окружностью;
7. Круг радиуса 2 с центром в
точке ![]() (точка
(точка ![]() и
окружность не включаются;
и
окружность не включаются;
8. Кольцо между окружностями
радиуса 1 и 3 с общим центром в точке ![]() (окружности
не включаются);
(окружности
не включаются);
9. Угол величиной ![]() с вершиной в точке
с вершиной в точке ![]() ,
расположенной выше действительной оси (стороны угла не включаются);
,
расположенной выше действительной оси (стороны угла не включаются);
10.Угол
величиной ![]() с вершиной в точке
с вершиной в точке ![]() ,
биссектрисой которого является отрицательная часть действительной оси (стороны
угла не включаются);
,
биссектрисой которого является отрицательная часть действительной оси (стороны
угла не включаются);
11.Прямая,
проходящая через середину отрезка, соединяющего точки ![]() и
и
![]() , перпендикулярно этому отрезку;
, перпендикулярно этому отрезку;
12.Парабола,
директрисой которой является мнимая ось, а фокусом - точка ![]() =1;
=1;
13.Эллипс с
фокусами в точках ![]() ,
, ![]() с
большой полуосью, равной
с
большой полуосью, равной ![]() ;
;
14.Гипербола
с фокусами в точках ![]() ,
, ![]() с
действительной полуосью, равной
с
действительной полуосью, равной ![]() ;
;
15.Внешность
круга ![]() ;
;
17. Правая
половина круга радиуса 1 с центром в точке ![]() ;
;
18. Угол
величиной ![]() с вершиной в точке
с вершиной в точке ![]() ,
стороны которого проходят через точки
,
стороны которого проходят через точки ![]() и
и ![]() ;
;
19. Часть
плоскости, лежащая с той же стороны параболы ![]() , что и
точка
, что и
точка ![]() и ограниченная этой параболой;
и ограниченная этой параболой;
20.
Полуплоскость, содержащая точку ![]() и ограниченная
касательной к окружности радиуса 1 и центром в нуле, проведенной в точке
и ограниченная
касательной к окружности радиуса 1 и центром в нуле, проведенной в точке 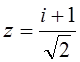 ;
;
5. 1. Окружность,
построенная на отрезке ![]() , как на диаметре.
, как на диаметре.
2. Окружность радиуса 1 с
центром в точке ![]() .
.
3. Действительная ось.
4. Окружность радиуса ![]() с центром в точке
с центром в точке ![]() .
.
6. 1. ![]() ,
, ![]() ; 2.
; 2.
![]() ,
, ![]() ;
;
7. 1.![]() >0; 2.
>0; 2.![]() >0,
>0, ![]() >0; 3.
>0; 3.![]() 2; 4.
2; 4.![]() <1; 5.
<1; 5.![]() <1,
<1, ![]() <0.
<0.
8. 1.
Расстояние от начала координат до точки ![]() ;
;
2.
Расстояние от мнимой оси до точки ![]()
3.
Расстояние от действительной оси до точки ![]()
9. Воспользоваться
определением выражения ![]() и тригонометрическими формулами.
и тригонометрическими формулами.
10. Воспользоваться формулой Эйлера.
11. Рассмотреть суммы: ![]() ;
; ![]() и т.д..
и т.д..
В задаче 6 воспользоваться формулой бинома Ньютона.
1. 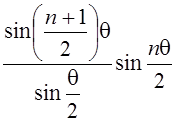 ;
;
2. 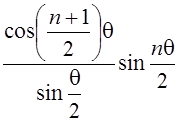 ;
;
3. 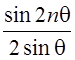 ;
;
4. 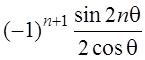 ;
;
6. 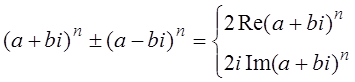 .
.
12. Исходить из определения равенства комплексных чисел.
1. 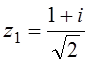 ,
, 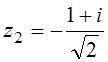 ;
;
2. ![]() ,
, ![]() ;
;
3. ![]() ,
, 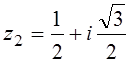 ,
, 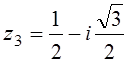 ;
;
4. 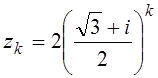 ,
, ![]() =0,1,2,3,4,5;
=0,1,2,3,4,5;
5. 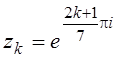 ,
, ![]() ;
;
6. 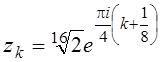 ,
, ![]() ;
;
7. ![]() =0,
=0, ![]() =1,
=1, ![]() ,
, ![]() ,
, ![]() ;
;
8. 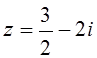 .
.
Решения.
2. 6. z=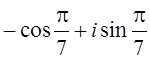 ; |z|=
; |z|=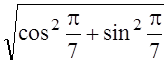 =1.
=1.
cosj=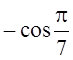 , sinj=sin
, sinj=sin![]() -
эти два соотношения определяют аргумент к.ч. z. Из второго равенства имеем j= (-1)k
-
эти два соотношения определяют аргумент к.ч. z. Из второго равенства имеем j= (-1)k![]() +kp, k-
целое. Из этого множества решений первому равенству удовлетворяют только углы,
расположенные во второй четверти, а именно: j=
+kp, k-
целое. Из этого множества решений первому равенству удовлетворяют только углы,
расположенные во второй четверти, а именно: j=![]() +2kp.
+2kp.
3. 9. Пусть z1=x1+iy1,
z2=x2+iy2. Вычислим
сначала ![]() :
:
![]() = (x1+x2)-i(y2+ y1).
Вычислим теперь
= (x1+x2)-i(y2+ y1).
Вычислим теперь ![]() =(x1-iy1)+(x2-iy2)= (x1+x2)- -i(y2+ y1).
=(x1-iy1)+(x2-iy2)= (x1+x2)- -i(y2+ y1).
11, 13, 14. Выражения, записанные под этими номерами, являются определениями тех кривых, которые приведены в ответах.
4.
16. Re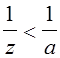 , a>0.
Re
, a>0.
Re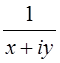 =Re
=Re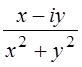 . Имеем:
. Имеем: 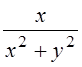 >
>![]()
![]()
![]() <ax
<ax![]()
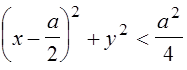 .
Следовательно, множеством точек, удовлетворяющих соотношению Re
.
Следовательно, множеством точек, удовлетворяющих соотношению Re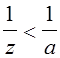 , является внутренность круга радиуса
, является внутренность круга радиуса ![]() с центром в точке
с центром в точке 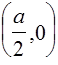 .
.
11. 5.
sin(a+b)+sin(a+2b)+![]() +sin(a+nb), a,b¹0 (mod 2p).
Выражение является мнимой частью суммы S=
+sin(a+nb), a,b¹0 (mod 2p).
Выражение является мнимой частью суммы S=![]() . Найдем ее. Заметим, что S- это сумма первых n членов геометрической прогрессии со знаменателем
. Найдем ее. Заметим, что S- это сумма первых n членов геометрической прогрессии со знаменателем ![]() , поэтому S=
, поэтому S=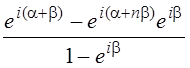 =
=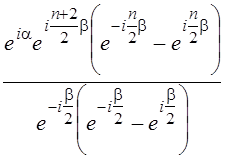 =
=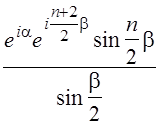 = =(cosa+isina)
= =(cosa+isina)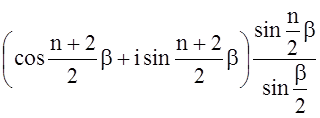 =
=
=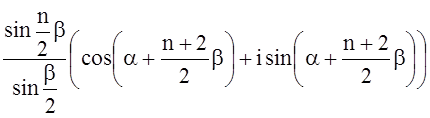
![]() ImS=
ImS=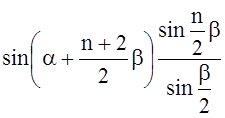 .
.
12. 8.
|z|-z=1+2i; Пусть z=x+iy Þ |z|=![]() . Уравнение
принимает вид:
. Уравнение
принимает вид: ![]() -x-iy=1+2i Û
-x-iy=1+2i Û 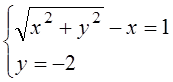 Û
Û 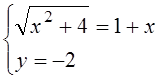 Û
Û 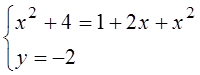 Û
Û 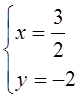 .
.
Следовательно,
решением является к.ч. 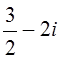 .
.
13. 1. Пусть равенство
имеет место![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Здесь мы воспользовались следующими свойствами корня из единицы, не равного единице (примитивного корня):
1. Степень примитивного корня с показателями 2,3,![]() ,
,![]() равна одному из
остальных примитивных корней
равна одному из
остальных примитивных корней ![]() .
.
2. Сумма всех корней ![]() -ой степени из единицы
равна нулю.
-ой степени из единицы
равна нулю.
Аналогично решается задача 2.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3
Тема: Последовательности и ряды комплексных чисел.
Для сходящейся
к числу ![]() последовательности
последовательности ![]() =
=![]() имеет место утверждение:
имеет место утверждение: ![]()
![]() и
и ![]() .
.
Достаточным
условием сходимости последовательности к.ч. являются следующее условие. Пусть ![]() , где
, где ![]() и
и ![]() .
.
Если ![]() и
и ![]()
![]()
![]() .
.
Для бесконечно
больших последовательностей (![]() ,
, ![]() ) справедливы следующие свойства:
) справедливы следующие свойства:
1. Если ![]() 0,
0, ![]() =1,2,
=1,2,![]() , то
, то ![]()
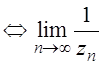 =0.
=0.
2. Если ![]() и
и ![]() , то
, то ![]() и
и 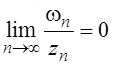 .
.
3. Если ![]() и
и ![]() , то
, то ![]() и
и 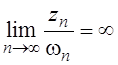 .
.
Для сходящегося ряда имеет место утверждение:
Ряд 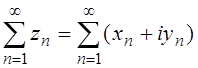 сходится тогда и только тогда, когда
сходятся ряды
сходится тогда и только тогда, когда
сходятся ряды 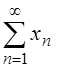 и
и 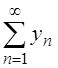 .
.
Радиус
сходимости ряда 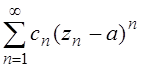 ,
, ![]() - к.ч.
- к.ч. ![]() =1,2,
=1,2,![]() определяется
формулой Коши-Адамара
определяется
формулой Коши-Адамара ![]() ,
, ![]() .
.
Ответить на вопросы.
1. Дать определение предела последовательности комплексных чисел.
2. Перечислить свойства сходящихся последовательностей.
3. Сформулировать критерий Коши сходимости последовательностей к.ч.
4. Доказать теорему Вейерштрасса: из любой ограниченной последовательности к.ч. можно выделить сходящуюся подпоследовательность.
5. Определить термин: "расширенная комплексная плоскость".
6. Дать определение предела
последовательности, равного ![]() .
.
7. Дать определение сходящихся, абсолютно сходящихся рядов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.