







Если система линейна, то система имеет единственный корень. Если нелинейна, то число корней может быть сколь угодно большим. Например,
Рис.1. Некоторое множество изолированных корней.
 |
При
положительном дефекте в случае линейной системы ![]() и
и ![]() множество
множество ![]() представляет
собой прямую, в случае
представляет
собой прямую, в случае ![]() – плоскость, при
– плоскость, при ![]() – многогранник типа конуса и т.д.
– многогранник типа конуса и т.д.
В
случае нелинейной системы при ![]() множество
множество ![]() представляет собой некоторую кривую, при
представляет собой некоторую кривую, при ![]() – поверхность, при
– поверхность, при ![]() и
более – конус.
и
более – конус.
При
![]() , исключив лишние ограничения, придем к
одному из рассмотренных вариантов или определим несовместность системы.
, исключив лишние ограничения, придем к
одному из рассмотренных вариантов или определим несовместность системы.
Вообще говоря, задачу (1) можно решать и приближенно, переходя к задаче с ограничениями в виде неравенств
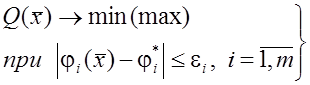
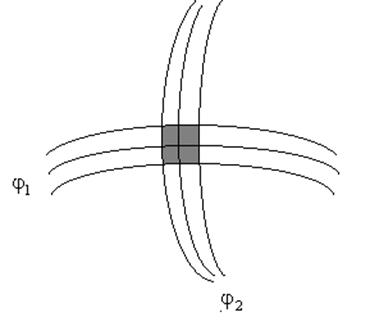 |
Рис.4.
При ![]() для решения задачи (1)
обычно, если это удается, поступают следующим образом. Пусть имеется
задача (1) с системой ограничений
для решения задачи (1)
обычно, если это удается, поступают следующим образом. Пусть имеется
задача (1) с системой ограничений
![]() ,
(2)
,
(2)
причем
![]() , т.е.
, т.е. ![]() . Систем
ограничений совместна и лишних ограничений нет. Тогда часть переменных, а
именно
. Систем
ограничений совместна и лишних ограничений нет. Тогда часть переменных, а
именно ![]() , выразим в явном виде из (2) через другие
, выразим в явном виде из (2) через другие ![]() , т.е.
, т.е.
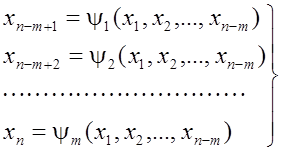 (3)
(3)
В
критерий ![]() вместо
вместо ![]() подставляем
выражения из (3)
подставляем
выражения из (3)
![]() .
.
В результате получаем задачу безусловной оптимизации меньшей размерности
![]() .
.
Следовательно, можем воспользоваться необходимыми условиями экстремума и найти решение задачи (1), решив систему
 .
(4)
.
(4)
Самое сложное при таком подходе разрешить систему
ограничений, представив ее в виде (3). Далеко не всегда удается получить
разрешение в форме (3) в элементарных функциях. Вопрос о том, когда функции ![]() существуют, дает теорема о неявных
функциях.
существуют, дает теорема о неявных
функциях.
Пусть все функции ![]() . Рассмотрим
первые частные производные этих функций. Эти производные можно рассматривать
как элементы прямоугольной матрицы размерности
. Рассмотрим
первые частные производные этих функций. Эти производные можно рассматривать
как элементы прямоугольной матрицы размерности ![]()
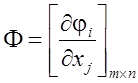 .
.
Из
нее можно выделить ![]() различных подматриц порядка
различных подматриц порядка ![]() . Например,
. Например,
 .
.
Эта
матрица называется якобианом функций ![]() по переменным
по переменным ![]() . Индекс
. Индекс ![]() указывает
на точку, в которой вычислены элементы якобиана.
указывает
на точку, в которой вычислены элементы якобиана.
Пусть
![]() множество индексов из числа
множество индексов из числа ![]() , не принадлежащих множеству
, не принадлежащих множеству ![]() .
.
Теорема о неявных функциях.
Пусть
![]() обладает следующими свойствами:
обладает следующими свойствами:
1.
В некоторой ![]() -окрестности точки
-окрестности точки ![]() функции
функции
![]() ,
, ![]() .
.
2.
![]() .
.
3.
Матрица ![]() -
неособенная.
-
неособенная.
Тогда
существует ![]() -окрестность (
-окрестность (![]() >0)
точки
>0)
точки ![]() из
из ![]() такая,
что для любой точки
такая,
что для любой точки ![]() из этой
из этой ![]() -окрестности
существуют однозначные и непрерывные в т очке
-окрестности
существуют однозначные и непрерывные в т очке ![]() функции
функции
![]() ,
, ![]() , …,
, …, ![]() , обладающие свойствами:
, обладающие свойствами:
А)
![]() ,
, ![]() .
.
Б)
При любом ![]() из
из ![]() -окрестности
-окрестности
![]() значения
значения ![]() ,
, ![]() , вычисленные по
, вычисленные по ![]() вместе
с компонентами вектора
вместе
с компонентами вектора ![]() образуют вектор
образуют вектор ![]() , удовлетворяющий
, удовлетворяющий ![]() .
.
В)
В ![]() -окрестности
-окрестности ![]() функции
функции
![]() дифференцируемы и при данных
дифференцируемы и при данных ![]() ,
, ![]() ,
производные
,
производные  являются единственным решением системы
уравнений
являются единственным решением системы
уравнений
 . (5)
. (5)
Выведем
необходимые условия, которым должна удовлетворять точка ![]() ,
доставляющая
,
доставляющая ![]() относительный максимум или минимум на
множестве
относительный максимум или минимум на
множестве
![]() .
.
Для того, чтобы в дальнейшем найти абсолютный максимум или минимум, необходимо вычислить все относительные оптимумы и выбрать наилучший.
Рассмотрим
для начала функцию двух переменных с одним ограничением. Пусть имеем ![]() ,
, ![]() .
Найдем необходимые условия, которым должна удовлетворять точка
.
Найдем необходимые условия, которым должна удовлетворять точка ![]() , если в ней достигается относительный
максимум (или минимум) при
, если в ней достигается относительный
максимум (или минимум) при ![]() .
.
Допустим,
что ![]() или
или ![]() не
равна нулю в точке
не
равна нулю в точке ![]() . Пусть
. Пусть 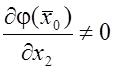 .
Тогда по теореме о неявных функциях существует
.
Тогда по теореме о неявных функциях существует ![]() -окрестность
точки
-окрестность
точки ![]() (
(![]() ), в
которой можем разрешить
), в
которой можем разрешить ![]() относительно
относительно ![]() так, что
так, что ![]() , где
, где ![]() - непрерывно дифференцируемая функция в
окрестности точки
- непрерывно дифференцируемая функция в
окрестности точки ![]() , и
, и ![]() .
.
Следовательно,
мы можем исключить ![]() в
в ![]() . Имеем
. Имеем
![]()
для
![]() . Но если
. Но если ![]() имеет в
точке
имеет в
точке ![]() относительный максимум при
относительный максимум при ![]() , то должно существовать такое число
, то должно существовать такое число ![]() ,
, ![]() , что
для всех
, что
для всех ![]() в
в ![]() -окрестности
точки
-окрестности
точки ![]() справедливо
справедливо
![]() .
.
Следовательно,
![]() имеет безусловный максимум в точке
имеет безусловный максимум в точке ![]() . (Аналогично для минимума).
. (Аналогично для минимума).
Сложная
функция ![]() дифференцируема в окрестности
дифференцируема в окрестности ![]() и
и
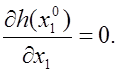 (6)
(6)
Дифференцируя
![]() как сложную функцию, получим
как сложную функцию, получим
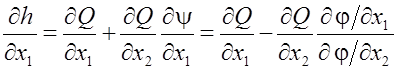 , так
как по теореме о неявных функциях
, так
как по теореме о неявных функциях
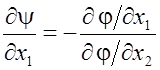 .
.
Из (6) следует
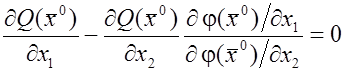 .
.
Обозначим
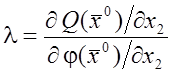 .
.
Таким
образом, необходимо, чтобы точка ![]() удовлетворяла
уравнениям
удовлетворяла
уравнениям
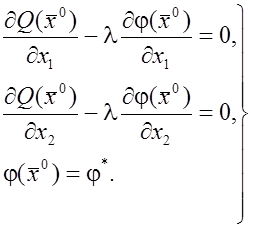
![]() (7)
(7)
Т.е.
удовлетворяла системе 3-х уравнений с тремя неизвестными: ![]() ,
, ![]() и
и ![]() .
.
Решив
систему, найдем все точки, где ![]() достигает
относительного максимума или минимума при
достигает
относительного максимума или минимума при ![]() .
.
Необходимые условия (7) удобнее получать, составив следующую функцию
![]() (8)
(8)
и
приравняв 0 ее частные производные по ![]() ,
, ![]() и
и ![]() .
.
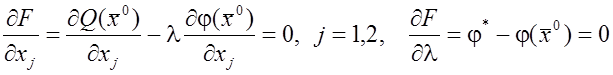 .
.
Функцию
![]() называют функцией Лагранжа, а
называют функцией Лагранжа, а ![]() - множителем Лагранжа.
- множителем Лагранжа.
 |
![]() - относительный
минимум
- относительный
минимум
Рассмотрим общий случай с ![]() переменными
и
переменными
и ![]() ограничениями. Пусть в точке
ограничениями. Пусть в точке ![]() функция
функция ![]() имеет
относительный максимум или минимум для
имеет
относительный максимум или минимум для ![]() . Далее
предположим, что в точке
. Далее
предположим, что в точке ![]() ранг матрицы
ранг матрицы
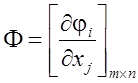
равен
![]() . Для простоты будем считать, что матрица
. Для простоты будем считать, что матрица ![]() является неособенной (первые
является неособенной (первые ![]() столбцов).
столбцов).
Тогда
по теореме о неявных функциях существует ![]() -окрестность
точки
-окрестность
точки ![]() такая, что для каждой точки
такая, что для каждой точки ![]() из этой
из этой ![]() -окрестности
можно разрешить уравнения
-окрестности
можно разрешить уравнения
![]() ,
, ![]() , относительно
, относительно
![]() ,
,
![]() ,
, ![]() , причем
функции
, причем
функции ![]() непрерывно дифференцируемы в окрестности
точки
непрерывно дифференцируемы в окрестности
точки ![]() и
и
![]() ,
, ![]() .
.
Функция
![]()
имеет
в точке ![]() безусловный относительный максимум или
минимум. Поэтому
безусловный относительный максимум или
минимум. Поэтому
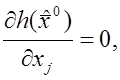
![]() .
(9)
.
(9)
По правилу дифференцирования сложной функции
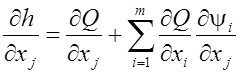 ,
, ![]() .
(10)
.
(10)
По
теореме о неявных функциях производные ![]() ,
, ![]() , для каждого
, для каждого ![]() представляют
собой решение системы уравнений
представляют
собой решение системы уравнений
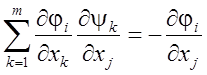 ,
, ![]() .
(11)
.
(11)
Имеем
![]() таких систем. Можно, конечно, решить
систему (11) и результаты подставить в (10). Но поступим следующим образом.
Рассмотрим набор чисел
таких систем. Можно, конечно, решить
систему (11) и результаты подставить в (10). Но поступим следующим образом.
Рассмотрим набор чисел ![]() ,
, ![]() ,
являющийся решением системы
,
являющийся решением системы ![]() уравнений
уравнений
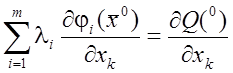 ,
, ![]() .
(12)
.
(12)
Решение этой системы существует и единственно, так как
матрица коэффициентов ![]() по предположению неособенная.
Умножим
по предположению неособенная.
Умножим ![]() -е уравнение из (11) на
-е уравнение из (11) на ![]() и просуммируем по
и просуммируем по ![]() .
Для каждого
.
Для каждого ![]() ,
, ![]() ,
получаем
,
получаем
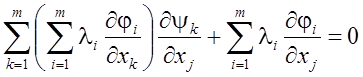 . (13)
. (13)
Из (9) и (10) следует
 ,
, ![]() .
(14)
.
(14)
Вычислим
(13) в точке ![]() и вычтем из (14), получим
и вычтем из (14), получим
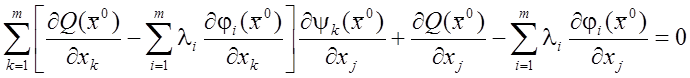 ,
,
![]() . (15)
. (15)
Отсюда, используя (12), имеем
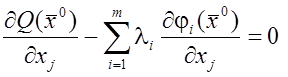 ,
, ![]() .
(16)
.
(16)
Объединив
(16) с (12) и ограничениями, получим, что точка ![]() , в
которой достигается относительный максимум или минимум должна удовлетворять
следующей системе из
, в
которой достигается относительный максимум или минимум должна удовлетворять
следующей системе из ![]() уравнений
уравнений
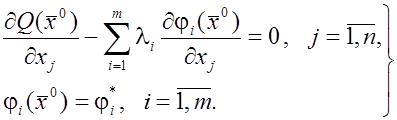 (17)
(17)
Каждая
точка ![]() , в которой достигается относительный
максимум или минимум при
, в которой достигается относительный
максимум или минимум при ![]() , будет являться
решением системы (17).
, будет являться
решением системы (17).
Необходимые условия можно получить, составив функцию Лагранжа
 (18)
(18)
и
приравняв 0 ее частные производные по всем ![]() ,
, ![]() , и по всем
, и по всем ![]() ,
, ![]() .
.
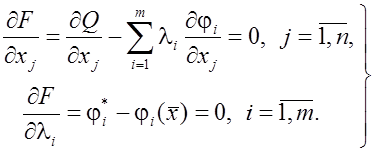 .
.
Построение таким образом необходимых условий называют методом
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.