Квадратичная модель.Алгоритм Федорова.

Вариант задания

Модель квадратичная на кубе со сторонами [-1,+1]. Строить D-оптимальные планы. Алгоритм Федорова.

Решение

Модель квадратичная на кубе: ,

.

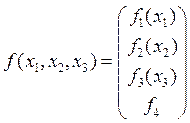Порядок решения:

1.  Строим вначале в качестве невырожденного начального плана D-оптимальный план по схеме: , где - число наблюдений.

2.  Тестируем алгоритм Федорова с целью выбора оптимальной сетки.

3.  В зависимости от числа точек плана анализируем качество полученных планов. Строим график.

1.  Строим невырожденный начальный план . Берем по минимуму значение числа точек в плане: , поскольку в данной модели число параметров равно 4.

С точки зрения этого алгоритма «оптимальная» сетка со 100 узлами, так как значение функционала максимальное из трех.

2. Запускаем алгоритм Федорова

С точки зрения максимума функционала, «оптимальна» сетка с количеством узлов 100.

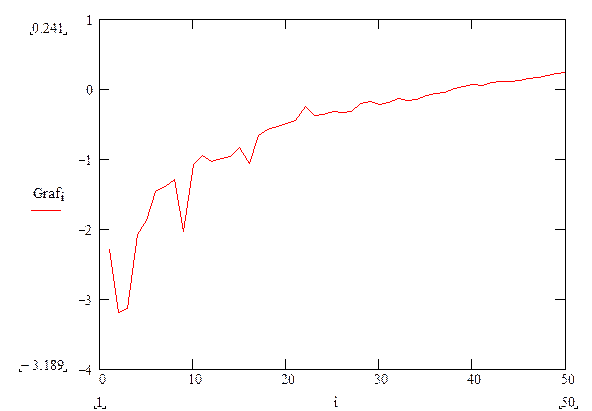
3. На оптимальной сетке построили график изменения функционала качества плана от числа точек в плане ( )