Каноническая матрица

Вариант задания:

Матрица обмена А:

0.2	0.1	0	0.3	0	0	0
0	0.2	0	0	0	0	0.5
0	0.2	0.5	0	0.9	0	0
0	0	0	0	0	0.4	0
0	0	0.5	0	0.1	0	0.2
0.8	0	0	0.7	0	0.6	0
0	0.5	0	0	0	0	0.3

Приведение к каноническому виду проводить по алгоритму 2.

Приведение матрицы к каноническому виду по алгоритму 2:

1. X1={2,3,4,5,7}

X2={4,5,6}

X3={1,2,4,6,7}

X4={2,3,5,7}

X5={1,2,4,6,7}

X6={1,2,3,5,7}

X7={1,3,4,6}

={1,2,4,6,7} m=5;

k=2;

n=7;

выполняется n=m+k;

1 неприводимое подмножество:X3,X5

2. X1={2,3,4,5,7}

X2={4,5,6}

X4={2,3,5,7}

X6={1,2,3,5,7}

X7={1,3,4,6}

={2,3,5,7} m=4;

k=3;

n=7;

2 неприводимое подмножество:X1,X4,X6

3. X2={4,5,6}

X7={1,3,4,6}

={4,6}       m=2;

k=2;

n=4;

неприводимое подмножество не выделяется

Делаем перенумерацию строк и столбцов:

3->1

5->2

1->3

4->4

6->5

2->6

7->7

Столбцы:

0	0	0.2	0.3	0	0.1	0
0	0	0	0	0	0.2	0.5
0.5	0.9	0	0	0	0.2	0
0	0	0	0	0.4	0	0
0.5	0.1	0	0	0	0	0.2
0	0	0.8	0.7	0.6	0	0
0	0	0	0	0	0.5	0.3

Строки:

0.5	0.9	0	0	0	0.2	0
0.5	0.1	0	0	0	0	0.2
0	0	0.2	0.3	0	0.1	0
0	0	0	0	0.4	0	0
0	0	0.8	0.7	0.6	0	0
0	0	0	0	0	0.2	0.5
0	0	0	0	0	0.5	0.3

Канонический вид матрицы A

Как видно, структура канонической матрицы обмена соблюдается.

1.  Найти устойчивое распределение дохода для неприводимых подмножеств

1) Неприводимое подмножество

Обозначим за A1:

С помощью Z-преобразования найдем . Рассмотрим матрицу :

Раскладываем полиномы по базису вида 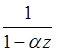 при помощи метода неопределенных коэффициентов:

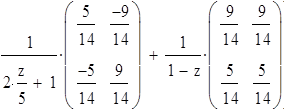
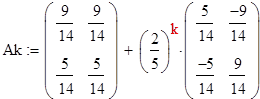
y_o=(1,1)^T

Устойчивое распределение дохода для первого неприводимого подмножества:

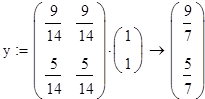
Обозначим за A2:

Второе неприводимое множество

С помощью Z-преобразования найдем . Рассмотрим матрицу :

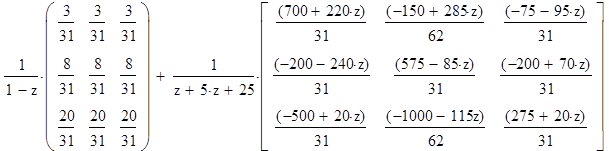
limA^k=, при k-> ∞

Устойчивое распределение дохода для второго неприводимого подмножества:

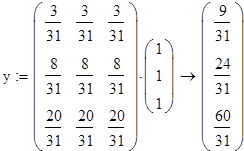
Посчитаем удельные доли доходов, отчисляемых из стран, не вошедших ни в одно неприводимое подмножество, в остальные страны:

µ₁=0.774

µ₂=0.839

µ₃=0.387

µ₄=0.

µ₅=0.

Проведем исследование модели при различном начальном распределении дохода и проверим правильность найденного устойчивого распределения дохода.

____________________________________________________________

_____________________________________________________________

_________________________________________________________

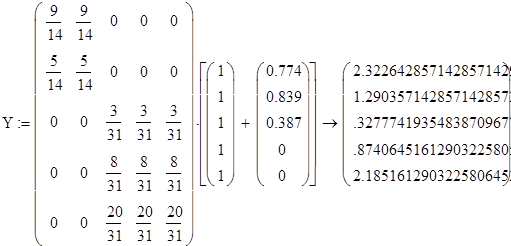
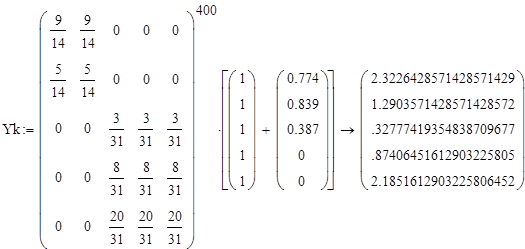
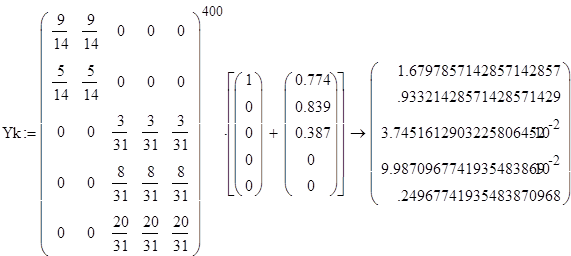
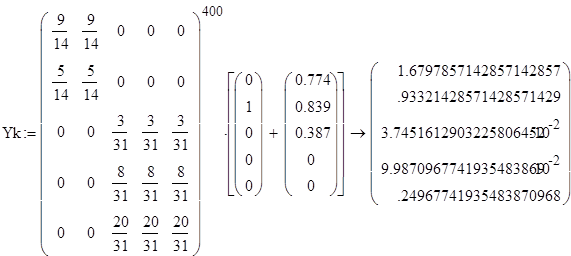
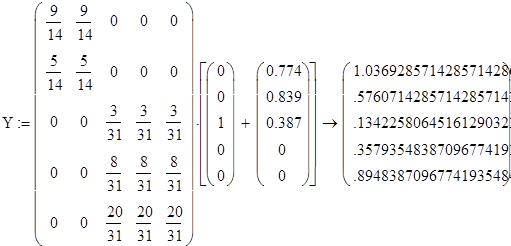
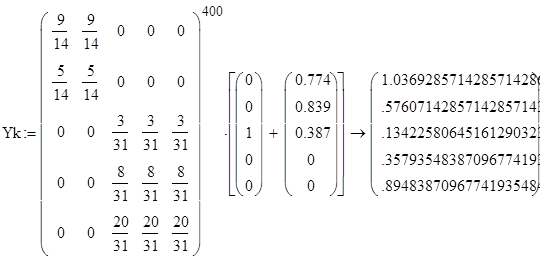
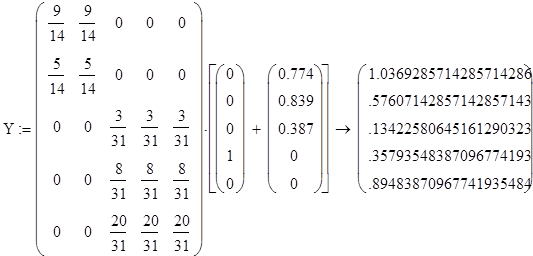
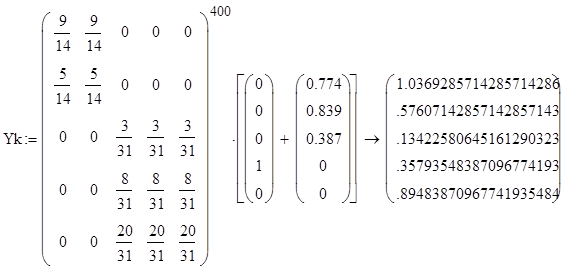
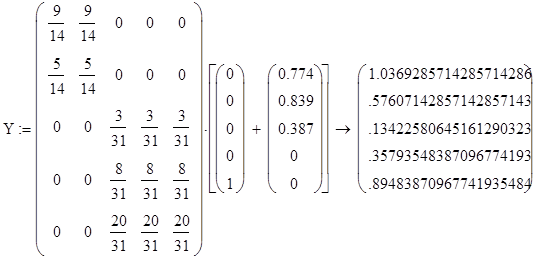
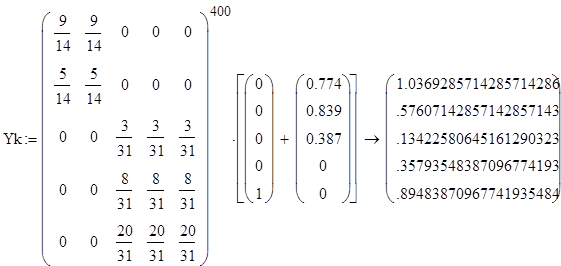
Стационарная матрица А совпадает с матрицей в каноническов виде, возведенной в степень 400, значит, преобразования были произведены правильно.

По проведенным исследованиям видно, что устойчивое распределение дохода не зависит от того, каково начальное распределение дохода между странами, попавшими в одно и то же неприводимое подмножество.