Исследование экономической или социологической системы с использованием методов регрессионного анализа.дисперсионного анализа

МОРФ

НГТУ

Кафедра Прикладной математики

Курсовая работа по дисциплине

“Методы планирования и анализа в экономических и социологических исследованиях”

Группа:             ПМ–04

Студент:           Штабель Е.

Вариант:           5

Преподаватель:        Еланцева И.Л.

Полетаева И.А.

Новосибирск, 2004 г.

1.  Цель задачи

          Исследование экономической или социологической  системы с использованием методов регрессионного анализа.дисперсионного анализа    

2.  Постановка задачи

Запишем общую модель регрессионного анализа в виде:

y=Xθ + ε, где           y – N-вектор значений отклика,

N – количество проведенных экспериментов;

y_i – значение отклика в i-ом эксперименте;

θ – p-вектор неизвестных параметров;

X – (N x p)-матрица планирования ранга r ;

ε - вектор ошибок,  ε ~ N (0, σ²I).

Используя данную модель и методы регрессионного анализа можно  оценить θ, проверить значимость факторов, что и будет проделано нами в дальнейшем.

Оценка параметров производится по методу наименьших квадратов:

 отсюда следует, что

Перед этим предлагается прошкалировать данные, т.е. чтобы вектор y и столбцы матрицы X имели единичные нормы.

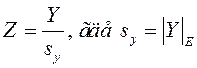
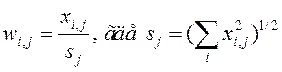
Находятся оценки  для шкалированной системы по формуле

Оценки  получаются из оценок  по формуле:

Проверка гипотезы о не значимости параметра H:

Имеет вид 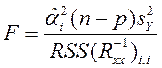 должна иметь распределение , где  уровень значимости. Если больше, то гипотеза отвергается.

-диагональный элемент матрицы обратной к .

RSS- остаточная сумма квадратов, равная

3.  Текст программы    

// kurs_pe.cpp : Defines the entry point for the console application.

//

#include "stdafx.h"

#include "stdio.h"

#include "math.h"

double a=cos(1.);

class scala

{

int n,m;

double **x,*y;

double **W,*Z;

double **R,*r;

double *teta;

double *tetaY;

double *tmpnorm;

double *diR;

int init();

int scaling();

double Norm(double *);

void print(double **,double *,int,int);

void gauss(double **,double *,double *);

void preobrazovanie();

void proverka_gipotez();

void obrtX(double **);

int solve_r();

public:

scala();

~scala();

int solve();

};

scala::scala()

{

diR=NULL;

y=NULL;

Z=NULL;

r=NULL;

teta=NULL;

tetaY=NULL;

tmpnorm=NULL;

};

scala::~scala()

{

if( y != NULL)delete [] y;

if( Z != NULL)delete [] Z;

if( r != NULL)delete [] r;

if( tmpnorm != NULL)delete [] tmpnorm;

for(int i=0;i<n;i++) delete [] x[i];

delete [] x;

for(int i=0;i<n;i++) delete [] W[i];

delete [] W;

for(int i=0;i<m+1;i++) delete [] R[i];

delete [] R;

if( teta!= NULL)delete [] teta;

if( tetaY != NULL)delete [] tetaY;

if( diR != NULL) delete [] diR;

};

int scala::init()

{

FILE *fd;

fd=fopen("init.txt","r");

if(fd!=0)

{

fscanf(fd,"%d %d",&n,&m);

fclose(fd);

}

else

{

printf("Not found file 'init.txt'");

return 0;

}

y= new double [n];

Z= new double [n];

fd=fopen("y.txt","r");

if(fd!=0)

{

for(int i=0;i<n;i++)fscanf(fd,"%lf",&y[i]);

fclose(fd);

}

else

{

printf("Not found file 'y.txt'");

return 0;

}

x= new double* [n];

for(int i=0;i<n;i++) x[i]= new double [m+1];

W= new double* [n];

for(int i=0;i<n;i++) W[i]= new double [m+1];

fd=fopen("x.txt","r");

if(fd!=0)

{

for(int i=0;i<n;i++)

{

x[i][0]=1;

for(int j=1;j<m+1;j++)

fscanf(fd,"%lf ",&x[i][j]);

}

fclose(fd);

}

else

{

printf("Not found file 'x.txt'");

return 0;

}

return 1;

}

void scala::print(double **X,double *Y,int k1,int k2)

{

for(int i=0;i<k1;i++) printf("%lf\n",Y[i]);

printf("\n");

for(int i=0;i<k1;i++)

{

for(int j=0;j<k2;j++)printf("%lf ",X[i][j]);

printf("\n");

}

}

int scala::scaling()

{

int i,j;

double norm=Norm(y);

tmpnorm= new double [m+1];

for(i=0;i<n;i++) Z[i]=y[i]/norm;

for(j=0;j<m+1;j++)

{

for(tmpnorm[j]=0,i=0;i<n;i++)

tmpnorm[j]+=x[i][j]*x[i][j];

for(i=0;i<n;i++) W[i][j]=x[i][j]/sqrt(tmpnorm[j]);

}

return 1;

}

int scala::solve_r()

{

int i,j,k;

double s;

R= new double* [m+1];

for(i=0;i<m+1;i++) R[i]= new double [m+1];

r= new double [m+1];

for(i=0;i<m+1;i++)

for(j=0;j<m+1;j++) R[i][j]=0;

for(i=0;i<m+1;i++)

{

for(j=0;j<m+1;j++)

{

for(s=0,k=0;k<n;k++) s+=W[k][i]*W[k][j];

R[i][j]=s;

}

}

for(i=0;i<m+1;i++)

{

for(r[i]=0,j=0;j<n;j++) r[i]+=W[j][i]*Z[j];

}

return 1;

}

double scala::Norm(double *a)

{

int i;

double s;

for(s=0,i=0;i<n;i++) s+=a[i]*a[i];

return sqrt(s);

}

void scala::proverka_gipotez()

{

int i,j;

double RSS,F,sy=Norm(y),*y_=new double [n];

///////////////---RSS-----/////////////////////////

for(i=0;i<n;i++)

for(y_[i]=0,j=0;j<m+1;j++) y_[i]+=x[i][j]*tetaY[j];

for(RSS=0,i=0;i<n;i++)  RSS+=(y_[i]-y[i])*(y_[i]-y[i]);

printf("\nОстаточная сумма квадратов:\t%lf\n",RSS);

for(i=0;i<m+1;i++)

{

F=teta[i]*teta[i]*(n-m-1)*sy*sy/(RSS*diR[i]);

printf("\nF[%d]=%lf ",i,F);

}

delete [] y_;

}

void scala::gauss(double **A,double *X,double *F)

{

int i,j,jmax;

double max;

for(i=0;i<m+1;i++)

{

for(jmax=i,max=fabs(A[i][i]),j=i+1;j<m+1;j++)

if(fabs(A[j][i])>max)

{

max=fabs(A[j][i]);