Исследование распределения статистик, используемых в различных приложениях статистических методов

Задания для индивидуальной работы по курсу “Применение математических методов и ЭВМ к решению научных, инженерных и экономических задач”

Цель работы: Методами компьютерного моделирования исследовать распределения статистик, используемых в различных приложениях статистических методов. Исследовать робастность выводов, осуществляемых с использованием данных процедур проверки гипотез (т.е. нечувствительность к малым отклонениям от предположений).

Тема 1.

Исследование распределений статистик, связанных с параметрами нормального закона

1. Исследовать распределение статистики 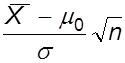, используемой при проверке гипотезы :  и наблюдаемом нормальном законе. Смоделировать распределение статистики для случаев известного  и неизвестного  ( будет оцениваться по той же выборке). В первом случае при нулевой гипотезе , соответствующей нормальному распределению, статистика должна подчиняться стандартному нормальному распределению, во втором – t-распределению Стьюдента с n степенями свободы. Провести исследование распределения статистики, если наблюдаемый закон не является нормальным, а более или менее близок к нему, например, является логистическим или Лапласа.

2. Исследовать распределение статистики 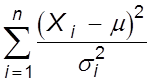, используемой при проверке гипотезы :  и наблюдаемом нормальном законе. Смоделировать распределение статистики в случае известного  и при неизвестном  ( будет оцениваться по той же выборке). В первом случае при нулевой гипотезе , соответствующей нормальному распределению, статистика должна подчиняться -распределению, во втором – -распределению. Провести исследование распределения статистики, если наблюдаемый закон не является нормальным, а более или менее близок к нему, например, является логистическим или Лапласа.

Тема 2.

Исследование распределений статистик непараметрических критериев согласия

В данном случае предусматривается моделирование “предельных” (и при заданных конечных объемах выборок) законов распределения статистик непараметрических критериев для различных сложных гипотез (при различных методах оценивания) и последующая идентификации полученных эмпирических законов.

Под идентификацией понимается выбор такого теоретического закона распределения (аналитической зависимости), который наиболее хорошо согласуется с эмпирической функцией распределения.

Результаты такого моделирования позволят в каждом конкретном случае (законе, к которому предполагается принадлежность выборки; объеме выборки; количестве и типе оцениваемых параметров; методе оценивания; используемом критерии) построить закон распределения статистики, используя который можно будет в дальнейшем принимать решение о соответствии или несоответствии наблюдаемой выборки случайной величины предполагаемому закону.

В общих чертах алгоритм численного моделирования выглядит следующим образом.

1. Моделируется (имитируется) n выборок заданного объема в соответствии с заданным законом распределения.

2. По каждой выборке в соответствии с используемым методом оцениваются параметры этого закона распределения (один при известном втором, второй при известном первом или одновременно оба, что соответствует 3-м различным сложным гипотезам).

3. Вычисляется значение соответствующей статистики.

4. По накопленной выборке значений статистики объема N анализируется полученное эмпирическое распределение статистики и осуществляется его идентификация.

Идентификация распределения возможна с использованием программной системы [1].

Псевдослучайная величина, принадлежащая закону с функцией распределения , может имитироваться по методу обратных функций, при котором случайная величина , подчиняющаяся закону с функцией распределения , получается в соответствии с соотношением , где  - функция, обратная к , а  - случайная величина, равномерно распределённая на интервале [0,1]. В качестве датчика равномерно распределенных псевдослучайных чисел можно использовать стандартный датчик, реализованный в C++. Соотношения, используемые для моделирования некоторых случайных величин приведены в [1].

Статистики, используемые в непараметрических критериях