Исследование движения нелинейного осциллятора

                                  (1)

Требуется:

1.  Определить частоту собственных линейных колебаний системы.

2.  Исследовать линейный резонанс в системе, положив частоту вынужденных колебаний равной частоте собственных линейных колебаний системы и .

3.  Построить аналитическое решение уравнения (1), считая . Ограничиться учётом членов порядка  .

4.  Построить аналитическое решение, соответствующее субгармоническому резонансу для случаев, когда  и .

5.  Построить численное решение уравнения (1).

5.1.           Рассмотреть случай .

5.2.           Рассмотреть случай .

5.3.           Рассмотреть случай .

5.4.           Построить полное решение уравнения (1).

5.5.           Для уравнения (1) при  построить решение, положив частоту вынужденных колебаний равной частоте собственных линейных колебаний системы.         

5.6.           Для случая 5.5 изучить устойчивость решений относительно малых вариаций начальных данных.

5.7.           Для полного уравнения (1) построить решение, положив частоту вынужденных колебаний равной частоте собственных линейных колебаний системы.

5.8.           При каком условии в уравнении (1) появляется субгармонический резонанс? Построить соответствующее численное решение для случая, когда  и .

5.9.           Когда в уравнении (1) может возникнуть параметрический резонанс? Построить соответствующее численное решение для случая, когда  и .

Таблица коэффициентов и значений начальных данных.

Порядок выполнения работы.

В нашем случае уравнение (1) имеет вид:

                                       (1`)

с начальными условиями:.

1.   Определение частоты собственных линейных колебаний системы.

Уравнение линейного осциллятора имеет вид:

, где  - частота собственных линейных колебаний. В нашем случае будет выглядеть как  

, где  — частота собственных колебаний.

2. Исследование линейного резонанса в системе, где частота вынужденных колебаний равна частоте собственных линейных колебаний системы и .

При  уравнение (1) принимает вид:

                                                        (2)           

Вместо этого уравнения рассмотрим соответствующее комплексное уравнение

,                                   (3)

где .  Характеристические числа (корни)  уравнения    равны 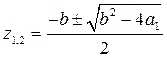,  при этом им соответствуют числа  правой части уравнения (3). Учитывая  равенство частоты вынужденных колебаний   и частоты собственных колебаний  , выполнение  равенства 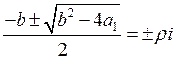 имеет смысл только при . Таким образом, нам требуется рассмотреть уравнение, имеющее вид:

.                                                                                  (4)

                                                                                 (5)

Решая соответствующее  комплексное уравнение (5) получаем частное решение:

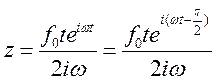, где , а частное решение уравнения (4) имеет вид:                                 

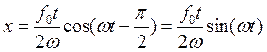
(6)

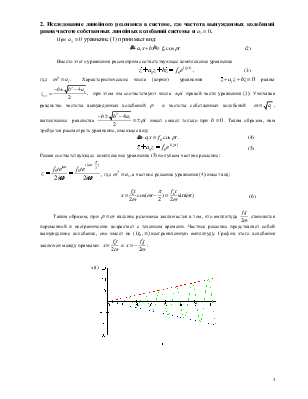
Таким образом, при  явление резонанса заключается в том, что амплитуда  становится переменной и неограниченно возрастает с течением времени. Частное решение представляет собой вынужденное колебание, оно имеет на (неограниченную амплитуду. График этого колебания заключен между прямым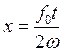и   и :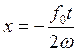

x(t)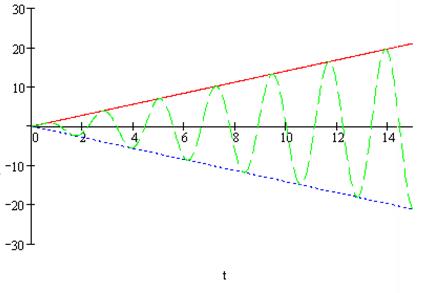                                          

3. Построение аналитического решения уравнения (1`), считая .

Строим аналитическое решение методом возмущений, подставляя решение х в виде ряда:

, где ε-малый параметр.

Подставляем в (1)  и получаем:

Собираем члены при степенях ε.

Находим х⁽⁰⁾ :

Решение будет представлять собой сумму общего решения однородного уравнения и частного решения неоднородного.

Обозначим .

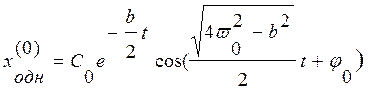
Подставим в уравнение:

Отсюда находим ;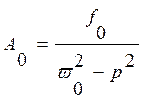  

Получаем общее решение для х⁽⁰⁾: .

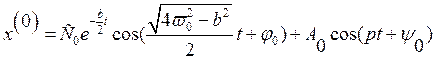Находим x⁽¹⁾:

;

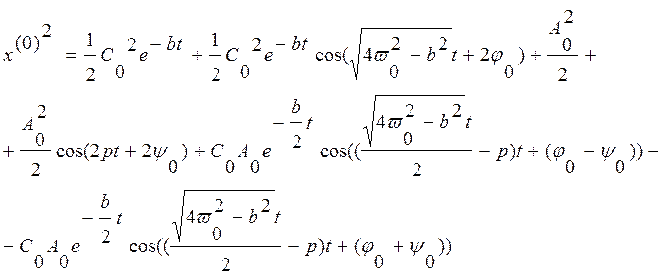
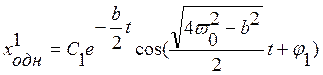Частное решение для первого слагаемого: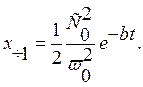      

Частное решение для второго слагаемого:

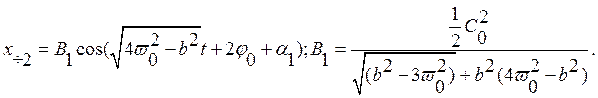
Частное решение для третьего слагаемого: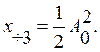     

Частное решение для четвертого слагаемого:

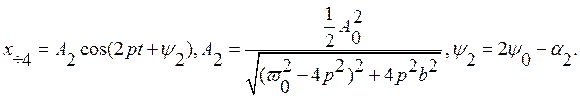
Частное решение для пятого слагаемого:

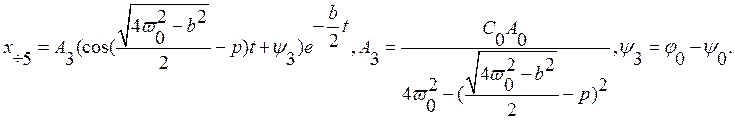
Частное решение для шестого слагаемого:

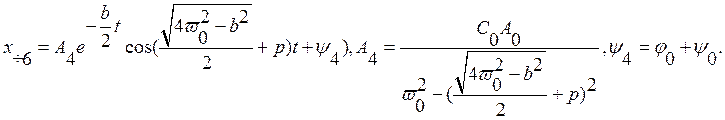
Таким образом получаем решение для х⁽¹⁾:

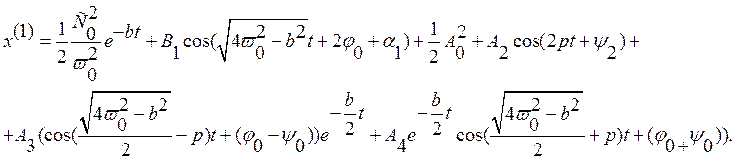
Коэффициенты  находятся из начальных данных: , а остальные коэффициенты выражаются через них.

4. Построение аналитического решения, соответствующего субгармоническому резонансу для случаев, когда   и .

Случай, когда  :

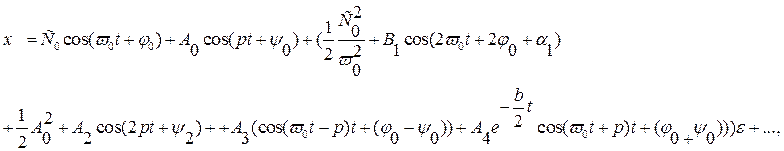
где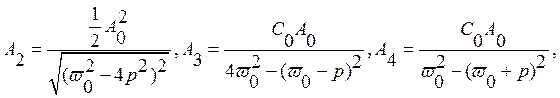

субгармонический резонанс возможен  при частоте .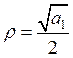

Случай, когда  :

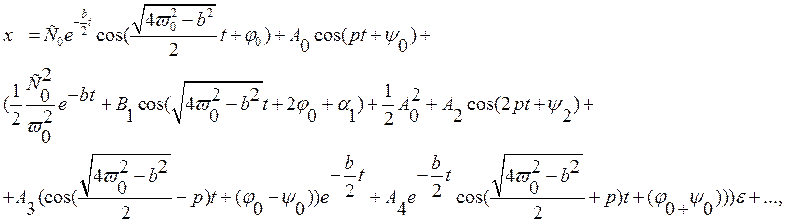
где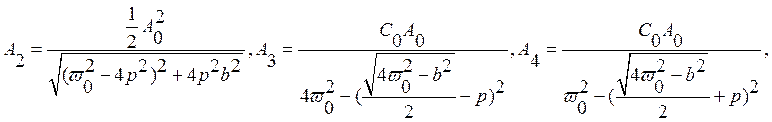

субгармонический резонанс возможен при частоте:

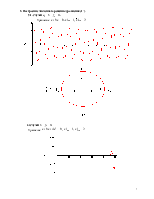
5. Построение численного решения уравнения (1`).

5.1. Случай .

Уравнение  ,

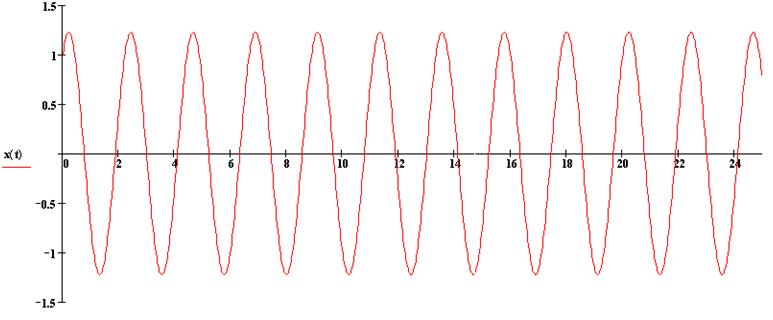
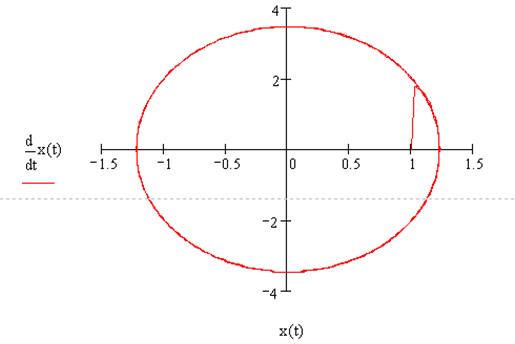
5.2 Случай .

Уравнение ,

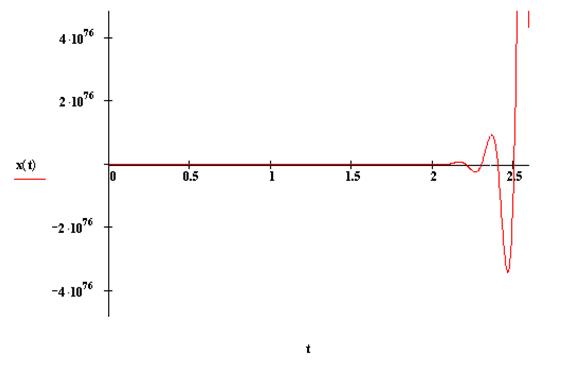
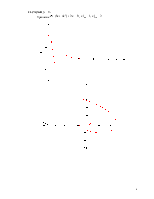
5.3 Случай .

Уравнение ,

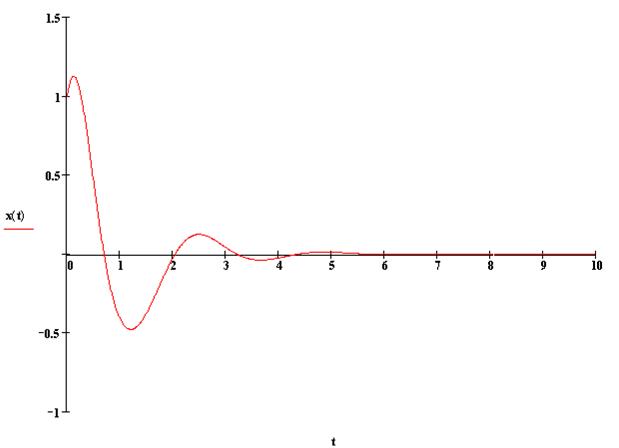
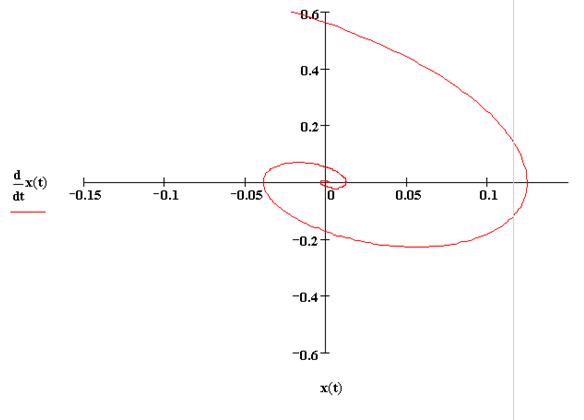
     5.4 Полное решение уравнения (1`).

Уравнение ,

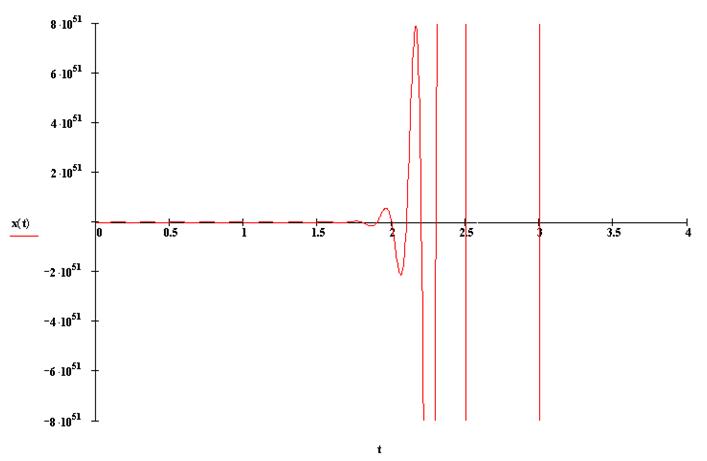
5.5.   Для уравнения (1`) при  построим решение, положив частоту вынужденных колебаний равной частоте собственных линейных колебаний системы.  

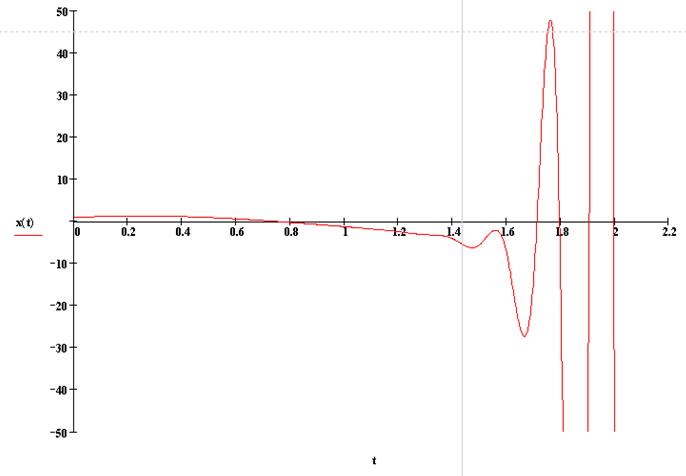
       5.6. Устойчивость решений  для случая 5.5 относительно малых вариаций начальных данных.

Положим, что .

При  получаем:

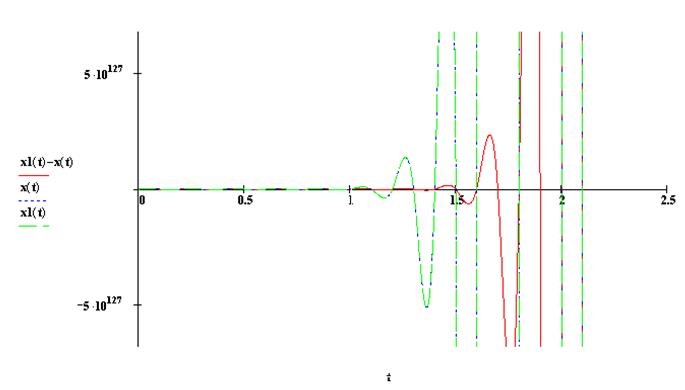
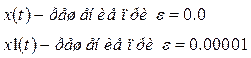
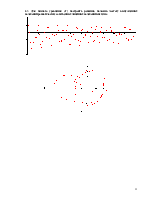
5.7. Для полного уравнения (1`) построить решение, положив частоту вынужденных колебаний равной частоте собственных линейных колебаний системы.

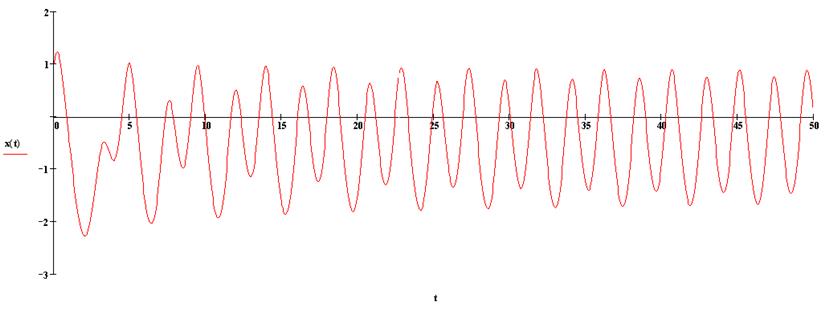
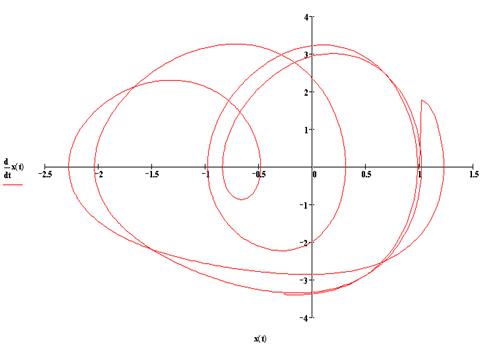
5.9.           Возникновение параметрического резонанса и соответствующее численное решение для случая, когда  и .

Возьмём вынуждающую силу на удвоенной частоте линейного осциллятора, получим: при

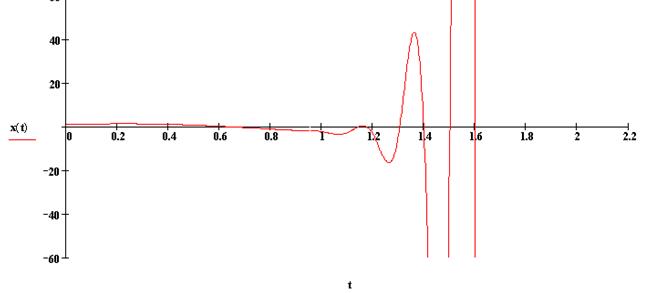
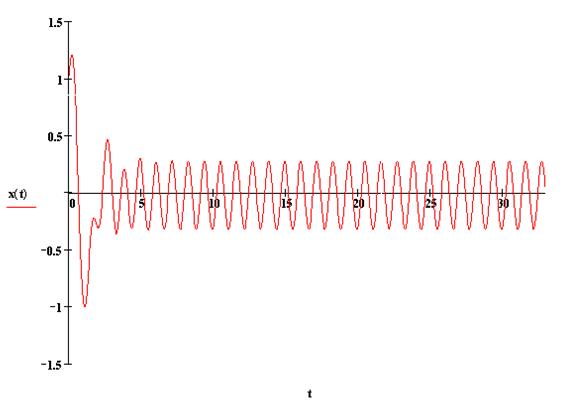
при