Искусственный интеллект. Методы моделирования. Стратегии. Логические выражения и предикаты.

опровержение может быть получено за конечное число применений принципа резолюций.

Вывод:

1. принцип резолюции является полным в смысле теоремы Робинсона (полным в  том смысле, что всегда получим решение);

2. принцип резолюции – непротиворечив (всегда  путь, который приводит к такому преобразованию, которое дает конечный результат)

10.Стратегии вывода с использованием резолюции. Стратегия упрощения.

Множество предложений упрощают, исключая из него некоторые предложения или из его предложений некоторые литералы. Такие упрощения позволяют снизить скорость роста числа новых предложений. Предложение можно исключить, если оно содержит уникальный литерал, т.е. литерал, не входящий с отрицанием ни в одно из предложений. Упрощения должны быть такими, чтобы упрощенное множество предложений было невыполнимо тогда и только тогда, когда невыполнимо исходное множество.

Стратегии упрощения:

а)   Стратегия исключения тавтологий;

б)   Стратегия исключения предложений, содержащих уникальный литерал;

в)   Стратегия использования подслучаев.

11.Стратегии вывода с использованием резолюции. Стратегия очищения.

К ним относятся методы доказательства (опровержения), при которых используются не все, а определенные резолюции. Разные стратегии очищения отличаются между собой правилом отбора предложений для резольвенций.

а)   Стратегия опорного множества: метод доказательства, при котором не допускаются резолюции двух аксиом.

б)   Стратегия линейного вывода: метод доказательства, использующий линейный вывод.

в)   Модальная стратегия: стратегия, где резолюции подвергаются только такие пары предложений, из которых хотя бы одно не удовлетворяется моделью.

3.   Стратегия упорядочения: к ним относятся стратегии, в которых не запрещаются никакие типы резольвенций, а лишь даются указания на то, какие из них надо выполнить в первую очередь. К этой стратегии относят стратегию наименьшего числа компонент, которая упорядочивает резолюции по числу литералов в получаемых резольвентах.

4.   Комбинированные стратегии: получаются комбинированием нескольких стратегий. Но следует иметь в виду, что хотя чистые стратегии являются полными, комбинированная стратегия, полученная на их основе, может оказаться неполной.

12. Принцип резолюции и его воплощение в прологе

Теорема о резолюции: Пусть  - формула в стандартной форме представления:  и пусть имеется формула  : . Тогда, если  противоречива, то и  - противоречива.

В языке Пролог знаки  не используются внутри предложений, а отрицания обозначаются –. Пролог автоматически производит разделение переменных в ходе последовательных резолюций. Все предложения, относящиеся к одному и тому же заключению (и, следовательно, соединенные знаком +), должны следовать друг за другом. Пролог позволяет использовать только предложения хорновского типа, т.е. такие предложения, которые содержат по крайней мере один положительный литерал, причем он должен находиться во главе предложения.

По отношению к резолюциям используется стратегия поддержки и замка. Пролог развертывает исследуемое дерево вначале в глубину, выделяя единственное отрицательное предложение. Остальные предложения обрабатываются в их естественном порядке. Литералы систематически исследуются, начиная слева направо. Для новой резолюции предпочтительно используется последняя полученная резольвента.

Выходной предикат становится единственным литералом. Ответ, выдаваемый Прологом, может быть не только константой, но и формальной переменной. Система типа пролог используется во всех пространствах, где деревья доказательства не слишком велики. Важная область применения системы – реализация запросов к базе данных. Системы типа Пролога, получив запрос, тут же начинают отыскивать ответы на него.

Другой областью, где находит применение Пролог, является управление роботами, которые способны решать задачи “в уме” и, исходя из этого, строить план действий. Тот же способ запоминания с помощью предикатов позволяет запоминать план, построенный с помощью резолюции.

13. Неклассические логические системы. Модальные логики. Временные логики.

Модальные логики:

L – модальный язык – это расширение языка логики предикатов  I-го порядка путём добавления двух операторов: □,◊ - модальные операторы.

Если F - формула логики предикатов 1-го порядка, то

□F ≡ ¬◊ ¬F   - отношение действительности

Логика знания и веры: □≡L  -“знаю”, LF  -“я знаю, что F - истина”

◊ ≡ М ≡ ¬L¬F  - “я не знаю, что не F ”.

Нормальная модальная система:

1) множество аксиом логики предикатов 1-го порядка;             2) аксиомы дистрибутивности  L(p→q) →(Lp→Lq)

3) правило modus ponens: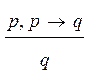, где p и q - формулы модальной логики;   

4) модальное правило вывода:;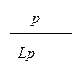  

Временные логики:

ПЛВ – псевдофизические логики времени. ВО- временные отношения.

Наряду с ПЛВ, модели времени, предназначенные для систем ИИ, должны содержать средства для описания шкал и операций над ними. Логика времени состоит из ядра ПЛВ и его расширения. Ядро ПЛВ, в отличие от его расширения, представляет собой проблемно-независимую часть и описывает алгебраические свойства и семантику базовых временных отношений. Ядро ПЛВ есть набор схем, правил вывода следующего вида: ; где -правильно построенные формулы языка ПЛВ.

14. Нормальная модальная система Т и её расширения до систем S4 и S5.

1.  множество аксиом логики предикатов I-порядка;

2.  аксиомы дистрибутивности;

, где - означает: я знаю, что - истинно.

3.  правило modus ponens: 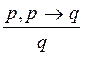, где  и - формулы модальной логики.

4.  Модальное правило вывода:  (если  истинно, то я знаю, что  истинно)

Системы S4(KT4), S5:

1.  аксиома T

2.  знание – это информация. То, что известно, то верно. Аксиома позитивной интроспекции:   (*)

наличие такой аксиомы даёт возможность формализации совершенного интроспективного интеллекта. Такая система обозначается S4 (KT4).

3.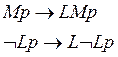    (**) (знак  - это отрицание)

Аксиома негативной интроспекции это система S5 – это такой совершенный интеллект, который отдает себе отчет в том, что он знает и в том, что не знает.

Система, обладающая такими свойствами:

         - рефлексия

15. Семантика возможных миров

Анализ истинности некоторой модальной формулы зависит