Изучение основных стратегий решения задач. Поиск пути в лабиринте.

Цель работы: Изучение основных стратегий решения задач. Приобретение  навыков  выбора  адекватных  стратегий в зависимости от типа задач. Выбор инструмента для реализации этих стратегий.

Задание

1.  Разработать адекватную структуру данных, максимально учитывающую специфику  предметной области задачи. Обосновать выбор структуры.

2.  Реализовать формальное описание проблемы на Прологе, снабдив программу достаточным количеством средств ввода - вывода для наглядного отображения результатов.

3.  Выделить пространство состояний и нарисовать граф переходов.

Вариант задания

Поиск пути в лабиринте.

1. Для представления каждой клетки лабиринта введем структуру v(integer; integer; integer; integer; integer), где на первом месте будет стоять: 0 – если на клетку можно ходить, -1 – если на клетку нельзя ходить, 1 – если клетка искомая. Пронумеруем все вершины, начиная с левой верхней. Остальные 4 числа – номера соседних вершин снизу, справа, сверху, слева соответственно или 0 если таковой нету. Весь лабиринт представим в виде списка структур типа v(). Расположим вершины в порядке их нумерации.

Поиск будем осуществлять рекурсивно в порядке перечисления соседей в структуре v() до нахождения первого попавшегося. Также введем список целых чисел, в котором будем хранить пройденные вершины.

2. Текст программы

domains

svaz=integer

versh=v(integer,svaz,svaz,svaz,svaz)

set=versh*

spisok=integer*

predicates

ver(set,versh,integer)

fd(spisok,set,versh,integer)

notin(spisok,integer)

clauses

notin([],_).

notin([H|T],A):-H<>A,notin(T,A).

fd(_,_,v(1,_,_,_,_),N):-write(N,' '),!.

fd(S,A,v(0,B,_,_,_),N):-B>0,notin(S,B),ver(A,Z,B),fd([B|S],A,Z,B),write(N,' '),!.

fd(S,A,v(0,_,B,_,_),N):-B>0,notin(S,B),ver(A,Z,B),fd([B|S],A,Z,B),write(N,' '),!.

fd(S,A,v(0,_,_,B,_),N):-B>0,notin(S,B),ver(A,Z,B),fd([B|S],A,Z,B),write(N,' '),!.

fd(S,A,v(0,_,_,_,B),N):-B>0,notin(S,B),ver(A,Z,B),fd([B|S],A,Z,B),write(N,' '),!.

ver([H|_],H,1).

ver([_|T],Z,N):-N1=N-1,ver(T,Z,N1).

goal

A=[v(0,-1,2,0,0),v(0,-1,3,0,1),v(0,6,0,0,2),

v(-1,0,0,0,0),v(-1,0,0,0,0),v(0,9,0,3,-1),

v(0,0,8,-1,0),v(1,0,9,-1,7),v(0,0,0,6,8)],

B=[v(0,-1,2,0,0),v(0,-1,3,0,1),v(0,-1,4,0,2),v(0,-1,5,0,3),v(0,10,0,0,4),

v(-1,0,0,0,0),v(-1,0,0,0,0),v(-1,0,0,0,0),v(-1,0,0,0,0),v(0,15,0,5,-1),

v(0,16,12,-1,0),v(0,17,-1,-1,11),v(-1,0,0,0,0),v(0,19,15,-1,-1),v(0,-1,0,10,14),

v(0,21,17,11,0),v(0,22,18,12,16),v(0,23,19,-1,17),v(0,-1,-1,14,18),v(-1,0,0,0,0),

v(1,0,22,16,0),v(0,0,23,17,21),v(0,0,-1,18,22),v(-1,0,0,0,0),v(-1,0,0,0,0)],

ver(B,Z,1),fd([],B,Z,1).

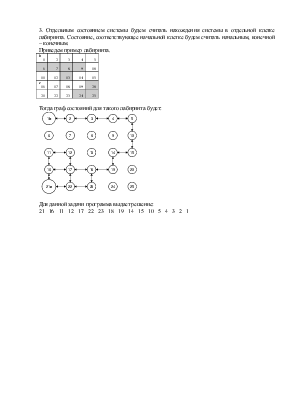
3. Отдельным состоянием системы будем считать нахождения системы в отдельной клетке лабиринта. Состояние, соответствующее начальной клетке будем считать начальным, конечной – конечным.

Приведем пример лабиринта.

Тогда граф состояний для такого лабиринта будет:

Для данной задачи программа выдает решение:

21   16   11   12   17   22   23   18   19   14   15   10   5   4   3   2   1