



1. Цель работы:
Изучение основных способов представления математических проблем в символьном виде, пригодном для формальной обработки на компьютере.
2. Задание
1. На примере программы символьного дифференцирования, прилагаемого к данной лабораторной работе, рассмотреть структуру данных для представления математических выражений.
2. Развить данную структуру для представления вещественных чисел, комплексных чисел.
3. Познакомиться с принципами лексического и синтаксического анализа входных строковых выражений, представляющих математические тексты.
4. Познакомиться с принципами трансляции из внутреннего представления математических выражений во внешнее – строковое.
5. Рассмотреть Пролог – программу для символьного дифференцирования и упрощения алгебраических выражений с точки зрения декларативной семантики (как систему аксиом)
6. Используя в качестве прототипа программу аналитического дифференцирования, составить программу аналитического интегрирования для выбранного класса функций.
3. Выполнение работы
Расширение используемой структуры данных для вещественных и комплексных чисел.
· Для поддержки и использования вещественных чисел в программе необходимо выполнить следующие модификации правил:
а) Правило elmexp(["-",TALSTR|IL],IL,int(INT)):-
str_int(TALSTR,INTp),
INT = -INTp. необходимо заменить на
elmexp(["-",TALSTR|IL],IL,int(INT)):-
str_real(TALSTR,INTp),
INT = -INTp.
б) Правило elmexp([TALSTR|IL],IL,int(INT)):-str_int(TALSTR,INT),!.
заменить на elmexp([TALSTR|IL],IL,int(INT)):- str_real(TALSTR,INT),!.
в) Правило преобразования выражения в строку вида:
strexp(int(INT),INTSTR) :- str_int(INTSTR,INT).
заменить на strexp(int(INT),INTSTR) :- str_real(INTSTR,INT).
г) В структуре данных, представляющей выражение EXP, заменить элемент
INT(INTEGER) на INT(REAL).
Для удобства чтения программы можно было бы заменить имя объекта числа в математическом выражении EXP с INT на FLOAT.
· Чтобы программа корректно обрабатывала комплексные числа, необходимо добавить ряд правил, учитывающих свойства мнимой единицы i
(i2 = -1, i3 = -i, …. ). Необходимо добавить в reducer правила:
multr(var(i),var(i),int(-1)).
multr(var(i),X,R):-multr(X,var(i),R),!.
multr(mult(X,var(i)),var(i),R):-!, multr(int(-1),X,R).
multr(var(i),mult(X,var(i)),R):-!, multr(int(-1),X,R).
Во всех остальных случаях i обрабатывается как константа.
· Для обработки вещественных чисел необходимо добавить дополнительные правила в reducer:
а) Ассоциативность умножения
multr(int(X),mult(int(Y),Z),mult(int(R),Z)):-!,R=X*Y.
multr(int(X),mult(Z,int(Y)),mult(int(R),Z)):-!,R=X*Y.
multr(mult(int(Y),Z),int(X),mult(int(R),Z)):-!,R=X*Y.
multr(mult(Z,int(Y)),int(X),mult(int(R),Z)):-!,R=X*Y.
б) Упрощение деления
multr(X,X,potens(X,int(2))):-!.
multr(X,Y,mult(X,Y)).
в) Нецелочисленное деление
divr(mult(int(X),V),int(Y),mult(int(Z),V)):-!,X/Y=Z.
divr(mult(V,int(X)),int(Y),mult(int(Z),V)):-!,X/Y=Z.
Разработка правил интегрирования.
Предикат интегрирования будет выглядеть следующим образом: i(EXP,EXP,EXP), где первый аргумент – исходное выражение, второй аргумент – выражение под дифференциалом (первоначально – var(“x”) ), а последний – результат интегрирования.
В программу включены правила, реализующие основные свойства интеграла, а также правила интегрирования некоторых функций (взяты из справочника интегралов):
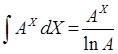 ,
, 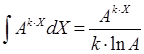 ,
, 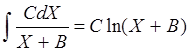 ,
, 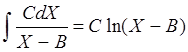 ,
,
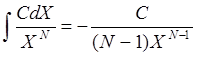 ,
, 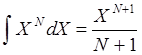 ,
, 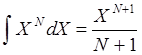 ,
тригонометрические функции.
,
тригонометрические функции.
Основные правила интегрирования:
i(int(C),X,mult(int(C),X)).
i(X,X,div(potens(X,int(2)),int(2))).
i(var(Y),var(X),mult(var(Y),var(X))):-Y<>X.
i(var(Y),V,mult(var(Y),V)):-Y<>"x".
i(plus(U,V),X,plus(U1,V1)):-i(U,X,U1),i(V,X,V1).
i(minus(U,V),X,minus(U1,V1)):-i(U,X,U1),i(V,X,V1).
i(mult(int(C),V),X,mult(int(C),V1)):-i(V,X,V1).
i(mult(var(Y),V),var(X),mult(var(Y),V1)):- X<>Y,i(V,var(X),V1).
i(div(V,int(C)),X,div(V1,int(C))):- i(V,X,V1).
Правила замены переменной:
i(mult(U,V),X,Z): -i(U,X,U1), i(V,U1,Z).
i(mult(U,V),X,Z):-i(V,X,V1),i(U,V1,Z).
Правила интегрирования по частям:
i(mult(mult(U,int(I)),V),X,mult(int(I),UV)):-
i(mult(U,V),X,UV).
i(mult(mult(int(I),U),V),X,mult(int(I),UV)):-
i(mult(U,V),X,UV).
i(mult(V,mult(U,int(I))),X,mult(int(I),UV)):-
i(mult(U,V),X,UV).
i(mult(V,mult(int(I),U)),X,mult(int(I),UV)):-
i(mult(U,V),X,UV).
i(mult(var(X),U),var(X),minus(mult(var(X),U1),U2)):-
i(U,var(X),U1),
i(U1,var(X),U2).
i(mult(potens(var(X),int(I)),U),var(X),minus(mult(potens(var(X),int(I)),U1),U2)):-
I1=I-1,
T=mult(potens(var(X),int(I1)),int(I)),
reduce(T,U3),
i(U,var(X),U1),
i(mult(U3,U1),var(X),U2).
4. Тестирование программы
Тест |
Результат |
0 |
0 |
1 |
x |
|
x +2 |
x^2/2+2*x |
|
(x+2)^4 |
(x+2)^5/5 |
|
2.2*sin(2*x) |
-1.1*cos(2*x) |
|
tan(x) |
-1*ln(cos(x)) |
|
1/x |
ln(x) |
|
i*i*2^x |
-1*2^x/ln(2) |
|
cos(x)*sin(x) |
sin(x)^2/2 |
|
x*sin(x) |
sin(x)-x*cos(x) |
|
x^2/4+1/x |
0.8333333*x^3+ln(x) |
|
2.5*sin(x)^2*cos(x) |
0.8333333*sin(x)^3 |
Анализируя результаты тестирования программы, можно сделать вывод, что существует непустое множество функций, на которых программа работает правильно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.