Задачи по теории вероятностей

Задачи по теории вероятностей

Билет №11

1)  В одной группе урн 3 белых и 2 черных шара, в другой 4 белых и 4 черных. Из первой переложили во вторую 2 шара. Какова вероятность, что из второй урны вынут белый шар?

2)  [0,2] и [p,2] в интервалах наугад выбирают две точки q и p.Вероятность , что qp<=1?

3)  X –случайная величина равномерно распределенная на [0,1] y – exp(1) Посчитать плотность распределения величины x+y?

Билет №23

1)  Какова вероятность взять из колоды хотя бы одного туза, если тянешь 3 карты из 36?

2)  Случайные величины q и p распределены равномерно в D : x²+y²<=1, y>=0, x>=0. Найти P(q,p)?

3)  Q, P – независимы. P{q=k}=P{p=k}=pq^(k-1), q=1-p. Найти мат. Ожидание Q при условии Q+P=L, где L=2?

Билет №25

1)  3 книги одного автора. Всего10 книг. Найти вероятность того, что книги одного автора стоят рядом?

2)  10 урн- 2б+2черных

5 урн-7белых +3черных выбираем на удачу урну и вытаскиваем шар.

Найти вероятность того, что белый, вероятность того что белый из второй урны?

3)  Кидали 3 монеты. Х – случайное событие – число решек. Найти закон                       распределения? Мх, Dх? Начертить график закона распределения и ф-ии распределения Р{x<3}-?

4)  Плотность распределения величины Х = С/(х⁴) Найти f(Y)? C-? P{0.1<Y<0.3}-?

1. На сборку поступают детали с 2-х автоматов, причём первый даёт 80% деталей.

1-й – 1% брака, 2-й – 4% брака. Найти вероятность, что 2-е проверенные детали окажутся бракованными. Какова вероятность, что при этом обе они изготовлены 1-м автоматом.

2. Положительные числа p и q случайным образом выбраны так, что их сумма не превосходит 3. Найти вероятность того, что корни уравнения  не существуют.
3. Найти , если  имеет нормальное распределение с параметрами
4. Найти , если  имеет показательное распределение.
Пусть X – время опоздания студента на лекцию, причём . С помощью неравенства Чебышева оценить вероятность того, что студент опоздает более чем на 5 минут.

Билет №19

1.  Независимые события. Формула суммы вероятности независимых событий.

2.  Биномиальное распределение: определение, обозначение, производящая функция, вывод  через производящую функцию.

3.  Корреляционные отношения и их связь с коэффициентами корреляции.

4.  Типы сходимости случайных величин; диаграмма.

5.  В урне 2б и 3ч шара. По очереди вынимают шары. Выигрывает тот, кто первым вытаскивает белый шар. Найти вероятность выигрыша первым и вторым игроками. Зависимы ли эти события.

6.  Детали делаются 3-мя автоматами. Первый делает 20%, второй делает 30%, третий – остальное. Брак первого 0,2%, второго – 0,3%, третьего 0,1%. Найти вероятность брака изделия. Найти вероятность того, что брак пошёл с 1-го автомата.

7. 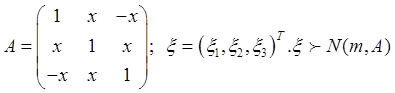 . При каких  это возможно?

8. 

9.   Найти плотность распределения Y. Показать, что X и Y не коррелированны.

1. 

2.  Отрезок . На нём точка A.

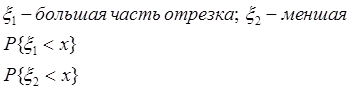
3. 

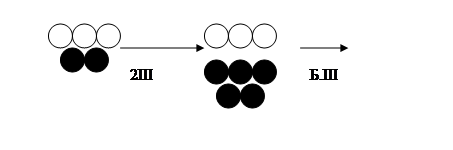
4.   

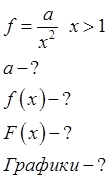
1.  Задача 60 из методички.

Свободная величина имеет непрерывную функцию распределения . Показать, что с. величина имеет равномерное распределение на .

2.  Найти , если  имеет нормальное распределение с параметрами

3.  стр187.

- что это обозначает не знаю, просто всё переписал как было.