Дифференциальные уравнения. Консервативная схема для нелинейного уравнения теплопроводности

Министерство образования Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра прикладной математики

Лабораторная работа № 2

Дифференциальные уравнения

Факультет: ПМИ

Группа: ПМ-12

Студент:  Дуркин Д.С.

Кичаева Н.А.

Преподаватель: Иткина Н.Б.

Новосибирск

2003

Задание: Построить консервативную схему для нелинейного уравнения теплопроводности:  с коэффициентами 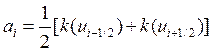,  с первыми краевыми условиями. Оценить порядок аппроксимации, устойчивость и сходимость.

Построение схемы:

Пусть дано стационарное одномерное уравнение теплопроводности:

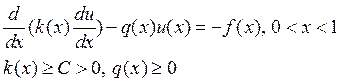
с первыми краевыми условиями: .

Тогда однородная консервативная схема будет иметь вид:

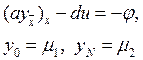
Коэффициенты этого уравнения будем вычислять по интервалам сетки .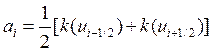

Пусть задана равномерная сетка с шагом h и узлы сетки  запишем консервативную схему в индексном эквиваленте:

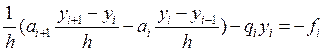
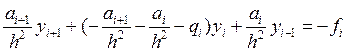
Таким образом, получаем систему уравнений:

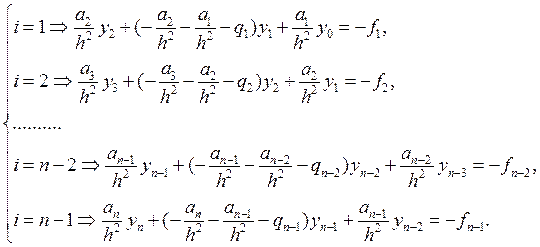
С учетом первых краевых условий

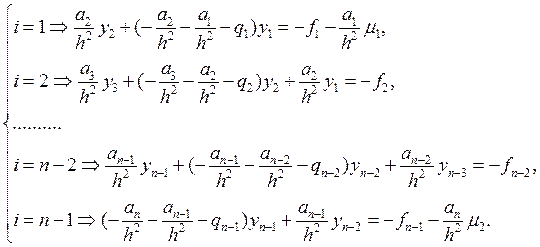
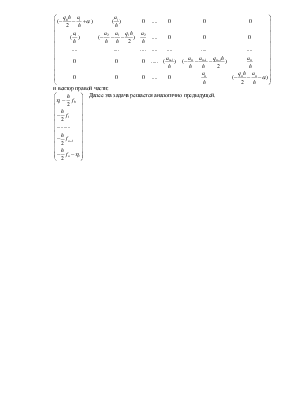
Отсюда получаем трехдиагональную симметричную матрицу вида

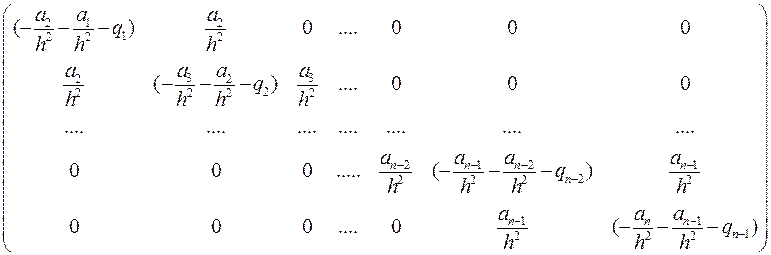
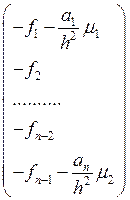
и вектор правой части:

Для решения полученной СЛАУ будем использовать метод LU разложения. Полученную матрицу будем хранить в диагональном формате и соответственно ему производить метод LU факторизации.

Теперь опишем способ получения элементов матрицы, используя условия задачи.

Каждый коэффициент  будем вычислять по формуле 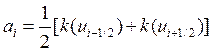. На сетке эта система будет иметь вид:

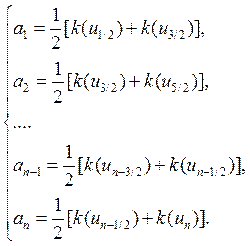При вычислении коэффициента , чтобы не выходить за границы сетки, вместо  будем использовать значение k в конечной точке отрезка.

Причем, с учетом условия нашей задачи и исходя из того, что 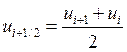, получаем

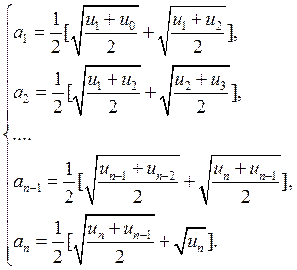
Теперьрассмотрим получение этой матрицы с учетом третьих краевых условий 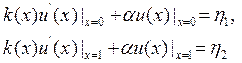: Получим  консервативную схему вида   где краевые условия учитываются следующим образом:

Проинтегрируем исходное уравнение теплопроводности на участке от 0 до h/2 и получим

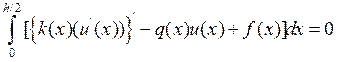
Тогда вычисляя интеграл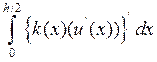 и приближая оставшиеся интегралы по формуле прямоугольников, получаем выражение:

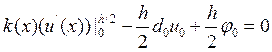
Учитывая, что 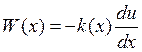, получаем  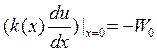и для h/2 соответственно: 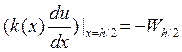, тогда из вида третьих краевых условий получаем 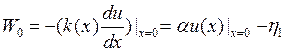. Поскольку интеграл мы рассматривали от 0 до h/2, то для точки h/2 центральная разность будет иметь вид правой разности  для точки 0, т.е

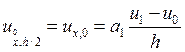 , а .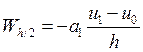

Рассматривая разность , получим первое уравнение СЛАУ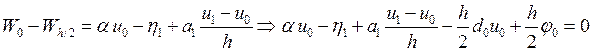

Группируя члены уравнения при  и учитывая условие, что , получим

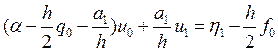
Аналогично рассматривая интеграл на отрезке от h/2 до 3h/2. получим следующее уравнение вида

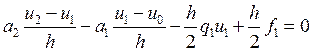
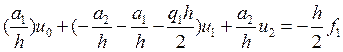
В итоге получаем следующую систему уравнений

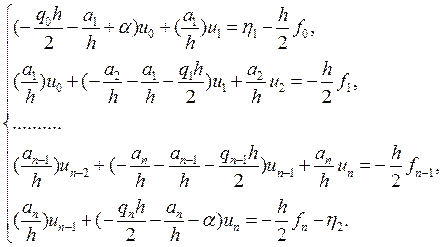
Отсюда получаем трехдиагональную симметричную матрицу вида

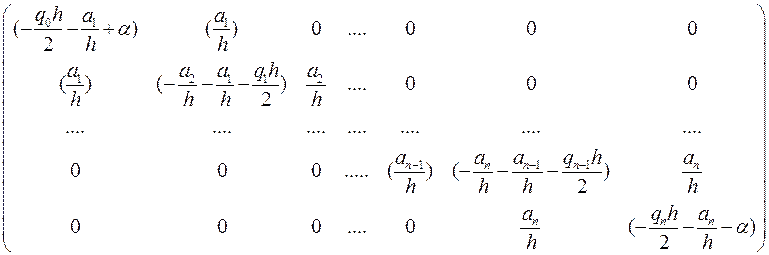
и вектор правой части:

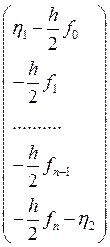Далее эта задача решается аналогично предыдущей.

Выводы:

Чтобы построить консервативную схему для стационарного одномерного уравнения теплопроводности, мы воспользовались методом баланса, т.е. интегрируя на интервалах сетки нашли соответствующие выражения  для нахождения коэффициентов схемы:

, ,  .

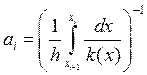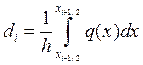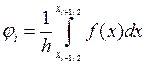Учитывая некоторые упрощения данных формул нахождения коэффициентов: ,а также то, что погрешность аппроксимации первых краевых условий равна 0, можно сделать вывод, что погрешность аппроксимации краевой задачи Дирихле  “идет” от  погрешности исходной схемы 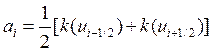.  Для задачи Неймана и задачи со смешанными краевыми условиями погрешность возникает также при аппроксимации самих краевых условий.

Интерполируя подынтегральные функции выбирая разностную схему для аппроксимации потока, мы можем получить тот или иной порядок аппроксимации исходной задачи.

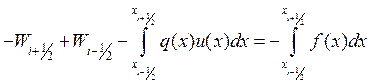
Поскольку поток рассматривается в полуцелых точках и аппроксимируется для них центральной разностью, то если порядок аппроксимации интегральных соотношений будет не ниже второго, то общий порядок аппроксимации схемы будет вторым. Для получения второго порядка аппроксимации интегралов выберем метод прямоугольников, в результате общий порядок аппроксимации схемы будет вторым.

Таким образом, если интерполировать полином нашей построенной консервативной схемой, то полином степени один должен считаться достаточно точно.

Что касается практических тестов, то величина порядка аппроксимации, оцененная по правилу Рунге  с использованием 3-х вложенных сеток варьируется от 1 до 2 в зависимости от вида приближаемого решения и линейности коэффициента  .

Для построения консервативной схемы с нелинейным коэффициентом , мы выбираем начальное приближение единичным и итерационно пытаемся аппроксимировать искомое решение.

Для полиномов степени не выше второй и линейного коэффициента   порядок аппроксимации приближается к 2. Если решение ведет себя как периодическая функция, то даже при линейном порядок аппроксимации снижается до 1.  Так же невысокий порядок аппроксимации получается при приближении экспоненты как резко возрастающей функции. Что касается тестов с нелинейным коэффициентом  , то опять-таки порядок аппроксимации оказывается более низким за счет нелинейности самого коэффициента .