Вычисление метрических характеристик основных процедур программы

6. ВЫЧИСЛЕНИЕ МЕТРИЧЕСКИХ ХАРАКТЕРИСТИК

ОСНОВНЫХ ПРОЦЕДУР ПРОГРАММЫ

Метрическими характеристиками программы или алгоритма называются соотношения, определяющие реализацию алгоритма. С помощью этих характеристик можно оценить алгоритм через внешние формы его проявления, независимо от языка программирования.

Практическое применение теория программометрики нашла в нормировании труда при серийном производстве, в оценивании времени разработки программы программистом (например, при принятии на работу), в оценивании количества ошибок в программе после ее написания и в других областях.

Если задана реализация алгоритма на каком-либо языке программирования, можно идентифицировать все операнды, определенные как переменные или константы, используемые в этой реализации, а также операторы, заданные в виде отдельных символов и их комбинаций, влияющие на значения и порядок операндов. Таким образом, мы получим словарь данной реализации, состоящий из простых операторов и операндов, используемых в программе, а по сумме всех операторов и операндов – длину реализации.

На основе словаря и длины реализации М.Х.Холстедом , [5], были получены метрические характеристики алгоритмов, пригодные для практического применения. Им также были введены следующие обозначения:

- число простых операторов;

- число простых операндов;

тогда  - размер словаря.                                                    (6.1)           

- общее число всех операторов, появляющихся в данной  реализации; 

- общее число всех операндов, появляющихся в данной  реализации;                                                                                              тогда - длина реализации.                                                 (6.2) 

Введем некоторые требования на длину реализации : , так как каждый символ словаря должен появиться в программе, по крайней мере, один раз – нижняя граница для ; - верхняя граница.

Длина реализации по словарю определяется Холстедом таким образом:

,                                                                   (6.3)

.                                                               (6.4)

Интерпретировать это уравнение можно по-разному. С одной стороны, это длина выражения любого алгоритма, а с другой – так как сумма двух логарифмов есть логарифм произведения, и первый множитель зависит от операторов, а второй от операндов, то длина может быть интерпретирована как двумерная величина, то есть как мера площади.

Важной характеристикой алгоритма является его размер, который меняется при переводе алгоритма с одного языка на другой, а также является различным для разных алгоритмов.

Соответствующая метрическая характеристика размера любой реализации какого-либо алгоритма, называемая объемом V, определяется как

          ,                                                           (6.5)

где - длина реализации, - ее словарь. Эта формула дает выражение объема в битах.

Реализация алгоритма в наиболее сжатой, «идеальной» форме, предполагает существование такого языка, в котором требуемая операция уже определена или реализована, возможно, в виде процедуры или функции. Таким образом, для реализации алгоритма на таком языке необходимы лишь имена операндов для его аргументов и результатов.

Введем следующие обозначения для параметров этого «минимального» языка:

- минимально возможное число простых операторов;                                 - минимально возможное число простых операндов, которое равно сумме входных и выходных параметров;

, ,                                                                    (6.6)

так как в минимальной форме ни операторы, ни операнды не требуют повторений. Минимально возможное число операторов для любого алгоритма , так как каждый алгоритм должен включать один оператор для имени функции и один в качестве символа присваивания или группировки. Тогда выражение для потенциального объема имеет вид:

.                                                    (6.7)

Зная объем программы и ее потенциальный объем, можно определить уровень программы :

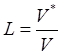.                                                                             (6.8)

Очевидно, с увеличением объема уровень программы уменьшается, и наоборот.

Если требуется определить уровень программы непосредственно из реализации, не зная чему равен ее потенциальный объем, используют следующую формулу для оценки уровня языка:

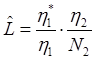.                                                                       (6.9)

Можно вычислить также коэффициент     интеллектуального содержания программы, воспользовавшись следующей формулой:

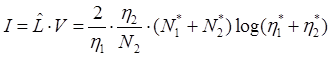.                                (6.10)

Этот коэффициент определяет количество информации в алгоритме.

Холстед ввел такое понятие как число элементарных мысленных различений, требуемых для порождения программы, а на его основе – понятие работы E. Если - число элементов в словаре, то - элементарное мысленное сравнение, необходимое для выбора одного слова, а величину 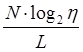 Холстед определяет как элементарное мысленное сравнение. Работу по программированию можно представить в виде:

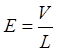,                                                                              (6.11)

где объем V равен числу мысленных сравнений, а - среднее число элементарных мысленных различений, входящих в каждое мысленное сравнение. Если подставить формулу (6.8) в уравнение (6.11) получим:

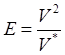,                                                                               (6.12)                         что мысленная работа по реализации алгоритма с данным потенциальным объемом в каждом языке пропорциональна квадрату объема программы.

Можно преобразовать уравнение (6.11) таким образом, чтобы работа по реализации алгоритма выражалась в единицах времени. Для этого разделим обе части уравнения на число различений в единицу времени. Считается, что в среднем человек способен примерно на 15-20 мысленных различений в секунду, и это число обозначают как S, S=18 (число Страуда). Таким образом, выражение для времени написания программы имеет вид: