Выбор наилучшей регрессии. Пошаговая регрессия

Министерство Образования Российской Федерации

Новосибирский Государственный Технический Университет

Курсовая работа по курсу:

 ”Методы планирования и анализа данных в

экономических и социологических исследованиях”

на тему: “Выбор наилучшей регрессии. Пошаговая регрессия”

Факультет: ПМИ

Группа: ПМ-03

Студенты: Лопарев С.

Преподаватели: Еланцева И.Л.

Новосибирск 2004

Цель работы:

Изучение метода пошаговой регрессии.

Задание :

Реализовать алгоритм пошаговой регрессии, протестировать данный алгоритм.

Описание метода:

Метод пошаговой регрессии состоит в том,  что на каждом шаге производиться либо включение в модель, либо исключение из модели какого-то одного регрессора. На каждом шаге один из регрессоров,  скажем , исключается, если при  его удалении RSS увеличивается на величину, не большую, чем умножение на  значение средней остаточной суммы квадратов . Другими словами регрессор  исключается на данном шаге,  если F- отношение для проверки гипотезы   в используемой в этот момент модели регрессии не превышает значения . Если такому условию удовлетворяет несколько регрессоров, то выбирается тот из них для которого увеличение RSS оказывается наименьшим (это равносильно наименьшему F - отношению). Если указанному условию не удовлетворяет ни один регрессор, то в модель включают регрессор, скажем  , введение которого уменьшает RSS на величину, не меньшую, чем умножение на     значение средней остаточной суммы квадратов, подсчитанной после включения  в модель. Иначе говоря, регрессор  включается на данном шаге в модель,  если F- отношение для проверки гипотезы   в модели, полученной добавлением этого регрессора к модели. Рассматриваемой на данном шаге, оказывается не меньшим, чем .И опять , если такому условию удовлетворяет несколько регрессоров, то в модель включается тот из них, который обеспечивает наибольшее уменьшение RSS( или что равносильно наибольшему  F – отношению). Процедура начинается с того, что подбираем  , а затем пытаемся ввести какой-нибудь регрессор.

Проверка гипотезы   - это проверка гипотезы о незначимости i-фактора. Для введения регрессора в модель будем использовать следующее значение F – отношения:

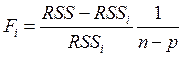, а для выведения регрессора из модели будем использовать следующее значение F – отношения:

.

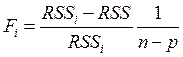О выбора значений F:

При использовании метода пошаговой регрессии мы сталкиваемся с задачей выбора значений  и .Обычно полагают , где  - некоторая произвольная константа. На каждом шаге мы стараемся не исключать регрессор, который только что ввели в модель, и не включать регрессор, который только что бал отброшен. Это будет обеспечиваться автоматически, если выбрать   .

Разработка программы

На вход программы подается файл regress.txt, в котором находиться количество регрессоров, количество наблюдений и собственно сама матрица регрессоров, размещенная там столбцами.

В файле y.txt значения отклика, в файле F.txt значение .

На выходе программы файл result.txt, в котором номера регрессоров в полученной модели и значения параметров  .

Для тестирования программы была выбрана исходная постановка задачи:

Инженер экономист, работающий на производстве, отвечает за снижение затрат. Наиболее важная статья расходов на его заводе – это ежемесячные затраты на воду. Он решил исследовать потребление воды с помощь 17 наблюдений за ее расходом и другими факторами.

Где    - среднемесячная температура, ,

- количество продукции, фунты,

- число рабочих дней в месяце,

- численность занятых на производстве рабочих,

- случайная составляющая,

- месячное потребление воды, галлоны.

Данные были взяты в книге:

[1]     Н. Дрейпер, Г.Смит. Прикладной регрессионный анализ: В 2-х томах. Том  2. – М: Финансы и статистика. 1987.

Тест № 1

При критическом значении получили модель с вхождением регрессоров , :    .

Т.е. на потребление воды влияет только количество рабочих и количество произведенной продукции.

Тест № 2

При критическом значении  получили модель с вхождением регрессоров  ,, , :      

Вывод

Имеются две разновидности метода пошаговой регрессии. Одна из них – это метод включения, в котором регрессоры не исключаются, а постепенно вводятся в модель. И метод исключения, который противоположен методы включения, т.е. в котором  сначала подбирается полная модель с m – регрессорами, а затем производится поочередное исключение регрессоров.

Однако оба этих метода могут приводить к разным моделям.     

Приложение

> restart:

> with(linalg):

with(plots):

> fd:=fopen("regress.txt",READ):

> m:=op(1,fscanf(fd,"%f")):

n:=op(1,fscanf(fd,"%f")):

> x1:=vector(n):

x2:=vector(n):

x3:=vector(n):

x4:=vector(n):

x5:=vector(n):

y:=vector(n):

> for i from 1 to n do

     x1[i]:=op(1,fscanf(fd,"%f"));

     x2[i]:=op(1,fscanf(fd,"%f"));

     x3[i]:=op(1,fscanf(fd,"%f"));

     x4[i]:=op(1,fscanf(fd,"%f"));

     x5[i]:=op(1,fscanf(fd,"%f"));

     y[i]:=op(1,fscanf(fd,"%f"));od:

> close(fd);

> fd:=fopen("F.txt",READ):

F0:=op(1,fscanf(fd,"%f"));od:

close(fd);

> Cp:=vector(m):

Rs:=vector(m):

AEV:=vector(m):

Ep:=vector(m):

> fcp:=(RSSp,sigma,p,n)-> RSSp/sigma+2*p-n;

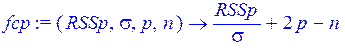
> fep:=(RSSp,p,n)->(1+n+p*(n+1)/(n-p-2))*RSSp/(n*(n-p));

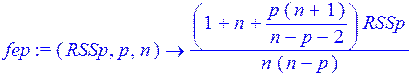
> faev:=(RSSp,p,n)-> p*RSSp/(n*(n-p));

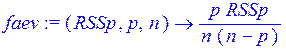
> y_avg:=add(y[i],i=1..n)/n:

centr:=add((y[i]-y_avg)^2,i=1..n):

> frs:=(yy)-> add((yy[i]-add(yy[i],i=1..n)/n)^2,i=1..n)/centr;

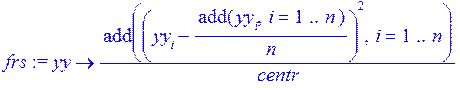
> f:= (i,j) ->

     if (j=1) then x1[i]

     else if (j=2) then x2[i]

          else if (j=3) then x3[i]

               else if (j=4) then x4[i]

                    else if (j=5) then x5[i]

                         end if

                    end if

               end if

          end if

     end if:

> X:=matrix(n,m,f):

> Xt:=transpose(X):

> thetaMNK:=evalm(evalm(inverse(evalm(Xt &* X)) &* Xt) &* y);

> yt:=evalm(X &* thetaMNK):

> RSST:=evalm(transpose(evalm(y-yt)) &* evalm(y-yt));

> sigma:=RSST/(n-m);

> Cp[1]:=fcp(RSST,sigma,m,n);

Rs[1]:=frs(yt);

Ep[1]:=fep(RSST,m,n);

AEV[1]:=faev(RSST,m,n);

> F:=vector(m):

RSS:=vector(m):

> f1:= (i,j) ->

     if (j=1) then x2[i]

     else if (j=2) then x3[i]

          else if (j=3) then x4[i]

               else if (j=4) then x5[i]

                    end if

               end if

          end if

     end if:

> X:=matrix(n,m-1,f1):

Xt:=transpose(X):

thetaMNK:=evalf(evalm(evalm(inverse(evalm