Выбор наилучшей регрессии. Метод включения

Министерство образования Российской Федерации

Новосибирский Государственный Технический Университет

кафедра прикладной математики

Курсовая работа

на тему:

«Выбор наилучшей регрессии. Метод включения»

по дисциплине:

«Методы планирования и анализа в

экономических и социологических исследованиях»

факультет:        ПМИ

группа:              ПМ-03

преподаватели: Еланцева И.Л.

Полетаева И.А.

студентка:          Радчикова Н.С.

Новосибирск

2004

Выбор наилучшей модели регрессии

Пусть значение исследуемого отклика описывается моделью

.

Поскольку мы обычно не располагаем информацией о виде , то собственно регрессионный анализ начинается с выбора класса допустимых решений -класс функций, в рамках которого предполагается вести поиск наиболее подходящей аппроксимации  для  в соответствии с тем или иным критерием качества модели.   Наиболее распространенными в статистической практике являются параметрические регрессионные схемы, когда в качестве допустимых решений выбирается некоторое параметрическое семейство функций . В этом случае дальнейший поиск  аппроксимации сводится к подбору значений параметров .

Выбор множества во многом неформализованная процедура. Помощь в выборе может оказаться решение следующих задач:

Ø  анализ априорной информации о содержательной сущности анализируемой зависимости (монотонность, экстремумы, асимптотичность, гладкость и т.д.);

Ø  анализ корреляционных полей , . Если предположить, что , то поиск наилучшей модели сведется к полному или направленному перебору всех моделей в с сравнением их по какому-либо критерию качества.

Среди наиболее часто используемых критериев можно выделить следующие:

Ø  -статистика Малоуса:

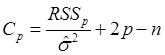, где

 - остаточная сумма квадратов, рассчитанная по модели с                  регрессорами;

- подходящая оценка для . Часто за не имением лучшего в качестве оценки неизвестной дисперсии берут 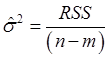, где - полное число регрессоров (модель из в этом случае имеет в своей структуре наибольшее число регрессоров).

Ø  -критерий:

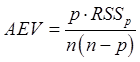
средняя дисперсия прогноза по всем точкам эксперимента.

Ø  коэффициент  детерминации: .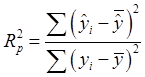

Ø  среднеквадратичная ошибка предсказания по  истинного значения отклика  (MSEP-критерий), где в качестве статистики для ее оценки используют величину:

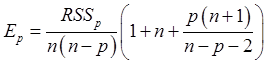
Большинство предлагаемых критериев являются функциями остаточной суммы квадратов RSS. При малом числе регрессоров RSS велика, а с добавлением новых – уменьшается. Постепенно скорость уменьшения  RSS замедляется, и после включения очередного числа (скажем ) регрессоров величина RSS становится почти постоянной. При числе регрессоров (неважно каких) регрессионное сглаживание превращается в интерполяционную схему с нулевой остаточной суммой квадратов.

Нахождение оптимальной модели  сводится к решению задачи структурной минимизации

, где - какой-либо критерий качества. Для более полного обоснования выбора     целесообразно указанную задачу решать с использованием различных .

Генерация модели. Метод включения.

Полным решением задачи нахождения  , очевидно, будет осуществление перебора всех моделей в с запоминанием лучших по различным критериям. Однако это довольно трудоемкая процедура и при  трудно реализуемая даже на современных компьютерах. На практике часто используют методы направленного перебора: метод включения и метод исключения.

В методе включения начинают с модели, состоящей из одного регрессора, например, свободного члена. Затем один за другим добавляют остальные регрессоры, а порядок их включения определяют по частным коэффициентам корреляции регрессоров с откликом. Регрессор, включенный на данном этапе, должен иметь максимальный частный коэффициент корреляции или частный -критерий. Частный -критерий для вводимого регрессора  вычисляется так

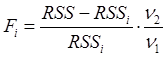, где , -остаточные суммы квадратов до и после включения в модель очередного регрессора: , .

Описание программы

Программа написана с помощью Maple 7.0.

Для запуска необходим файлы:

• nm.txt – заданы n и m
• x.txt – задание матрицы X.
• y.txt – задание вектора Y

Выходной файл rezult.txt.

Исходные данные

Данные для исследования взяты из книги Дрейпера Н. «Прикладной регрессионный анализ».  Упражнения 4  стр. 78:

номер наблюдения	скорость воздуха	температура охлаждающей воды	концентрация кислоты	потери аммиака
1	80	27	89	42
2	80	27	88	37
3	75	25	90	37
4	62	24	87	28
5	62	22	87	18
6	62	23	87	18
7	62	24	93	19
8	62	24	93	20
9	58	23	87	15
10	58	18	80	14
11	58	18	89	14
12	58	17	88	13
13	58	18	82	11
14	58	19	93	12
15	50	18	89	8
16	50	18	86	7
17	50	19	72	8
18	50	19	79	8
19	50	20	80	9
20	56	20	82	15
21	70	20	91	15

Текст программы:

restart:

with(linalg):

fd1:=open("c:/УНИВЕРСИТЕТ/Семестр9/Курсовик/COPY/nm.txt",READ): 

first:=readline(fd1):

second:=readline(fd1):

str:=sscanf(first,"%d"):

str1:=sscanf(second,"%d"):

n:=(op(str)):

m:=(op(str1)):

close(fd1):

x:=array(1..n,1..m):

fd2:=open("c:/УНИВЕРСИТЕТ/Семестр9/Курсовик/COPY/x.txt",READ):

for i from 1 to n

do

for j from 1 to m

do

first1:=readline(fd2):

strr:=sscanf(first1,"%g");

x[i,j]:=(op(strr)):

end do:

end do:

close(fd2):

fd3:=open("c:/УНИВЕРСИТЕТ/Семестр9/Курсовик/COPY/y.txt",READ):

y:=array(1..n):

for i from 1 to n

do

first1:=readline(fd3): strr:=sscanf(first1,"%g");

y[i]:=op(strr):

end do:

close(fd3):

fd4:=open("c:/УНИВЕРСИТЕТ/Семестр9/Курсовик/COPY/rezult.txt",WRITE):

regress:=array(1..m):

for i from 1 to m

do  regress[i]:=3:

end do:

p:=m:

xtemp:=array(1..n,1..p):

k:=0:  xtemp:=x:

tett:=evalf(multiply(inverse(multiply(transpose(xtemp),xtemp)),transpose(xtemp),y)):

ysk:=multiply(x,tett):

yysk:=evalm(y-ysk):

k1:=m:

RSS:=evalf(multiply(transpose(yysk),yysk)):

sigma:=RSS/(n-m):

for i from 1 to m

do regress[i]:=0:

end do:

regress[1]:=3:

p:=1:i:=1:

xtemp:=array(1..n,1..p):

xtemp:=submatrix(x,1..n,1..p):

tett:=evalf(multiply(inverse(multiply(transpose(xtemp),xtemp)),transpose