Вариационное исчисление. Уравнения Эйлера-Лагранжа

§1. Уравнения Эйлера-Лагранжа.

1084.  Найти достаточные условия сильного минимума интеграла

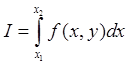
при условии, что конечные точки минимальной кривой лежат соответственно на прямых:  и  .

Примеры:

1).  

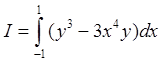
2).

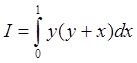
3).

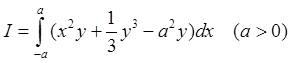
4).

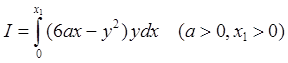
Указание:

Воспользоваться формулой Тейлора с остаточным членом.

1085.  Найти минимум интеграла

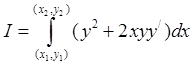
1086.  Найти экстремум интеграла

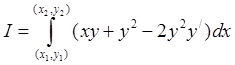
1087.  Найти экстремум интеграла

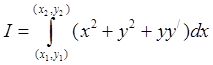
1088.  Найти экстремаль интеграла

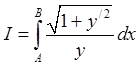
проходящую через заданные точки A и B, лежащие в верхней полуплоскости .

1091.  Найти экстремали интеграла 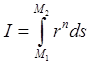 (в полярных координатах r, q), выражающего момент n-ой степени дуги  относительно начала координат.

1094.  Среди всех кривых, соединяющих начало координат с прямой , определить ту, которая, заключая вместе с осью и указанной прямой площадь заданной величины S, имеет наименьшую длину.

Указание:

Взять за независимую переменную 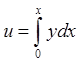, т.е. площадь, ограниченную кривой, осью и переменной ординатой (прием Эйлера).

1096.  Найти поверхность вращения около оси , имеющую заданную площадь и заключающую наибольший объем при условии, что поверхность пересекает ось вращения ровно два раза.

1097.  Найти все интегралы 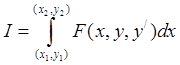, для которых экстремалями служат прямые линии.

Указание:

Составив дифференциальное уравнение экстремалей, , получить из уравнения Эйлера  дифференцированием по уравнение в частных производных для

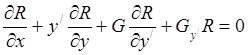
Т.о., существует бесчисленное множество задач вариационного исчисления, имеющих заданное уравнение своим уравнением Эйлера.

§2. Необходимые и достаточные условия для простейшей задачи вариационного исчисления.

1099.  Среди кривых, соединяющих точки A(1,3)  и B(2,5), найти ту, которая дает минимум интеграла

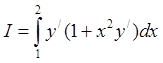
Указание:

Рассмотреть также полное приращение интеграла .

1101.  Среди линий, соединяющих точки A(1,0) и B(2,1), найти ту, которая дает минимум интеграла 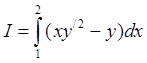. Найти характер минимума.

1105.  Показать, что прямая дает только слабый минимум интеграла 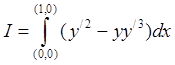, хотя условие Лежандра  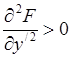в точках экстремали выполняется для всех

1109.  Найти минимум интеграла 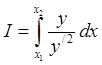. Найти экстремали, проверить условия Лежандра, Якоби, Вейерштрасса и найти характер минимума.

1113.  Найти в вертикальной плоскости  кривую, двигаясь по которой, тяжелая материальная точка придет в кратчайшее время из точки O(0,0)  в точку M(a,b); при этом дано, что начальная скорость в точке O равна .

§3. Параметрическая форма интегралов, трансверсальность.

1123.  Найти геодезические линии круглого цилиндра .

1128.  Имеем две окружности радиуса r с центрами в точках  и . Кривая лежит в верхней полуплоскости, кончаясь на данных окружностях, а при вращении вокруг дает поверхности наименьшей площади. В каких точках и под каким углом она пересекает окружности?

1132.  Среди линий, соединяющих точку O(0,0)  с кривой , найти ту, которая дает минимум интеграла

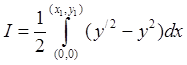
§5. Интегралы, зависящие от производных высших порядков или от нескольких функций.

1158.  Среди линий, проходящих через точки A(0,0) и B (1,0), найти ту, которая обращает в минимум интеграл 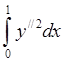в двух случаях:

1). Если ;

2). Если не дано никаких других условий.

1165.  Является ли  полной производной от функции и если это так, то найти функцию .

1173.  Показать, что уравнения Эйлера для интеграла допускают следующие первые интегралы:

1). 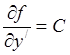, если f не содержит y

2). 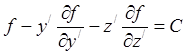, если f  не содержит x

§6. Разрывные решения. Односторонняя вариация.

1184.  Найти разрывные решения с угловой точкой для задачи о минимуме интеграла

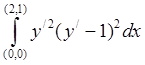
1185.  Среди линий, идущих из точки A(0,0) в точку B(2,0), найти линию с угловой точкой, вдоль которой интеграл 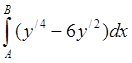 принимает минимальное значение.

§8. Изопериметрические задачи.

1223.  Найти форму тела вращения относительно оси , однородного, имеющего данный объем V и оказывающего наибольшее притяжение по закону Ньютона на точку, лежащую на пересечении тела с .

1226.  Из кривых длиной l , соединяющих точки   и , определить ту, которая вместе с  ограничивает наибольшую площадь. При этом .

1228.  Найти замкнутую кривую данной длины l , ограничивающую площадь наибольшей величины.

1232.  Из начала координат плоскости  провести кривую OA , длиной l , кончающуюся на прямой и образующую вместе с ординатой точки A и осью  наибольшую площадь.

1240.  Найти минимум интеграла 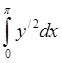, если 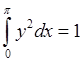, . Найти экстремали и проверить условие Якоби.

1244.  Из линий от точки A(0,0,0) до B(1,1,1), у которых

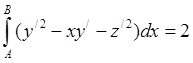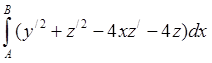, найти ту, у которой  - минимум. Рассмотреть такую же задачу при условии, что про точку A известно лишь, что она лежит в плоскости .