Анализ схем пар прогноз-корекция

Выводы по результатам вычислительных экспериментов.

Рассмотрим решения следующих тестовых задач:

1.  , решение:

2.  , решение:

3.  , решение: .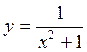

Каждая задача решалась с использованием 4-х пар прогнозов и коррекций на сетках с шагом h, h/2 и h/4. В целях чистоты эксперимента повторная коррекция не использовалась.

Схемы (пары прогноз-коррекция):

1. Неустойчивый прогноз 4-го порядка аппроксимации (A1=2), устойчивая коррекция 5-го порядка аппроксимации (A1=0.2).
2. Устойчивый прогноз 4-го порядка аппроксимации (A1=0.5), устойчивая коррекция 5-го порядка аппроксимации (A1=0.2)
3. Неустойчивый прогноз 5-го порядка аппроксимации, устойчивая коррекция 5-го порядка аппроксимации (A1=0.2)
4. Устойчивый прогноз 4-го порядка аппроксимации (A1=0.5), неустойчивая коррекция 6-го порядка аппроксимации.

Использование последней пары показало свою нецелесообразность (как и ожидалось), т. к. неустойчивая коррекция приводит к очень высокому росту погрешности и получение сколько-нибудь приемлемых результатов очень затруднительно, поэтому не будем его рассматривать. Другие пары показали вполне приличные результаты. Т. к.  устойчивость методов рассматривалась асимптотическая, исследования были проведены на сетках как с достаточно большим шагом (0.1) так и с шагом до 0.0025.  Рассмотрим полученные результаты и постараемся выделить метод, наиболее оптимальный для данных задач.

Схему №3 бракуем сразу, т. к. ее погрешность слишком велика () по сравнению с другими () на 1-й задаче, в то время как на других задачах она не дает выигрыша, несмотря на максимальный порядок аппроксимации прогноза. Сравнивая схемы №2 и №3, видим, что они дают очень близкие решения и ведут себя похоже. Но на задаче 2 схема №2 дает немного более точное решение (вероятно, сказывается устойчивость, и погрешность накапливается меньше). Таким образом, оптимальной схемой среди рассматриваемых можно признать схему №2, которая использует устойчивые прогноз и коррекцию, и, выбирая схему для решения какой-либо задачи, нужно обращать внимание на устойчивость, а не только на высокий порядок аппроксимации, т. к. неустойчивость может аннулировать это достоинство (как это видно на 3-й схеме). Так же коррекция должна соответствовать взятому прогнозу, т.е. ее порядок аппроксимации должен быть хотя бы на 1 больше, чем у прогноза для того, чтобы получить хорошие результаты.