Индивидуальная работа по дисциплине «Моделирование и управление в экономике»
Выполнил Мульцын К.А., ПМ-91, Вариант 18.
1. (г)
Написать алгоритм моделирования дискретной СВ, распределенной по отрицательному
биномиальному закону распределения: ![]()
1)
Берем ![]() как СВ, равномерно распределенную на
как СВ, равномерно распределенную на ![]() ,
, ![]()
2)
![]() , где
, где ![]() получены по
реккурентной формуле
получены по
реккурентной формуле ![]() ,
, ![]()
3)
Если ![]() , то
, то ![]() ,
,
Иначе увеличиваем ![]() и переходим на шаг 2
и переходим на шаг 2
4) Если нужно получить еще одну СВ, то переходим на шаг 1
Здесь 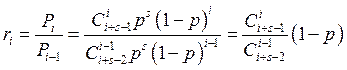 .
.
2. (и)
Найти методом обратной функции моделирующее выражение для СВ ![]() , с плотностью распределения
, с плотностью распределения ![]() ,
, ![]()
Найдем ![]() исходя из того факта, что
исходя из того факта, что 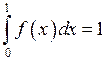
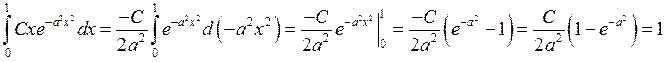
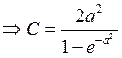
Найдем функцию распределения для этого закона:
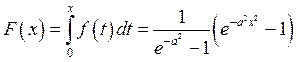
Найдем ![]() из уравнения
из уравнения ![]() , где
, где ![]()
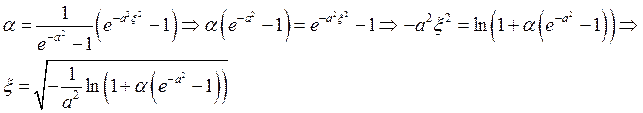
Выражение под корнем положительно, т.к. логарифм меньше нуля в
силу того, что ![]() , а
, а ![]()
3. (и)
Найти моделирующее выражение для СВ ![]() , имеющей плотность
распределения
, имеющей плотность
распределения 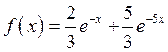 ,
, ![]() по
методу обратной функции, когда
по
методу обратной функции, когда ![]() немонотонна.
немонотонна.
Разобьем ![]() на сумму
на сумму ![]() , где
, где 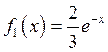 и
и 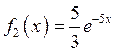 .
.
Найдем величины ![]() ,
, ![]() :
:
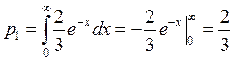
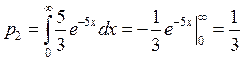
Соответствующие функции распределения:
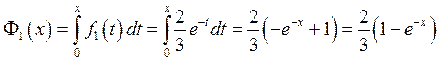
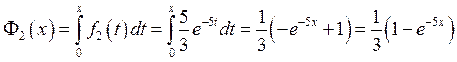
Найдем обратные функции:
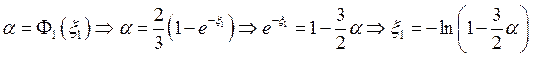
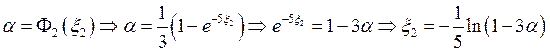
Алгоритм:
1)
Моделируем дискретную случайную величину ![]() с рядом
распределения
с рядом
распределения 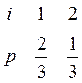
т.е. если ![]() и
и 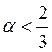 , то
, то ![]() , иначе
, иначе ![]()
2)
![]() , где
, где ![]()
4. (в)
Написать алгоритм моделирования СВ ![]() , распределенной с плотностью
, распределенной с плотностью
![]() ,
, ![]() с
использованием порядковых статистик.
с
использованием порядковых статистик.
Найдем ![]() из условия
из условия 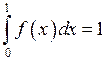 :
:
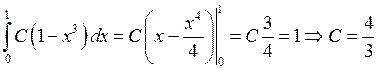
Представим плотность вероятности в виде полинома Бернштейна:
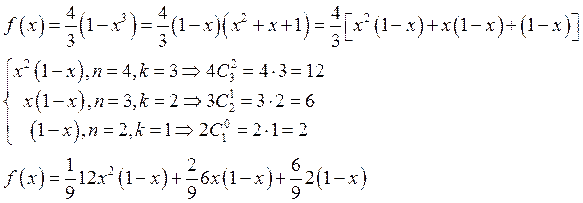
Алгоритм:
1)
Моделируем случайную величину ![]()
2)
Если 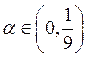 , моделируем 4 СВ и берем в качестве
, моделируем 4 СВ и берем в качестве ![]() 3-ью порядковую;
3-ью порядковую;
если 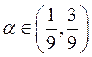 , моделируем 3 СВ и берем в к-ве
, моделируем 3 СВ и берем в к-ве ![]() 2-ю порядковую;
2-ю порядковую;
если 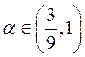 , моделируем 2 СВ и берем 1-ю
порядковую статистику.
, моделируем 2 СВ и берем 1-ю
порядковую статистику.
3) Если нужна еще одна СВ, то на шаг 1.
5. (б)
Написать алгоритм моделирования СВ ![]() с плотностью
распределения
с плотностью
распределения ![]() , где
, где ![]() и
и ![]() . Сделаем это по методу исключения.
. Сделаем это по методу исключения.
Найдем ![]() из условия
из условия 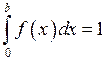 :
:
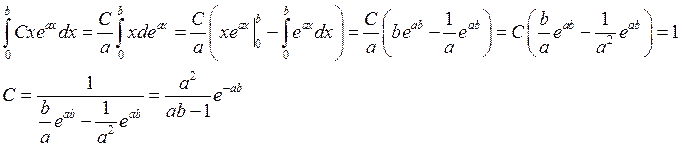
При ![]() (при
(при 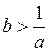 )
функция
)
функция ![]() возрастает, а в противоположном случае –
становится целиком отрицательной, что недопустимо для функции плотности
вероятности, следовательно случаи
возрастает, а в противоположном случае –
становится целиком отрицательной, что недопустимо для функции плотности
вероятности, следовательно случаи ![]() мы не рассматриваем. Но
тогда функция достигает своего максимума в точке
мы не рассматриваем. Но
тогда функция достигает своего максимума в точке ![]() и он
равен
и он
равен 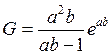 .
.
Алгоритм:
1)
Моделируем две СВ ![]() и
и ![]()
2)
Если ![]() , то
, то ![]() , иначе
на шаг 1
, иначе
на шаг 1
Событие шага 2 произойдет с вероятностью ![]() .
.
6. (б)
Написать алгоритм моделирования СВ ![]() с плотностью
распределения
с плотностью
распределения 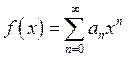 ,
, ![]() ,
, ![]() по методу суперпозиции.
по методу суперпозиции.
Функция плотности вероятности представима в виде, указанном в
теореме о методе суперпозиции: 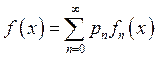 , где
, где 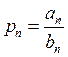 , а
, а ![]() , где
коэффициенты
, где
коэффициенты ![]() подбираются с тем условием, чтобы
подбираются с тем условием, чтобы 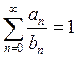 и
и ![]() . Тогда
алгоритм моделирования выглядит следующим образом:
. Тогда
алгоритм моделирования выглядит следующим образом:
1)
Моделируем дискретную СВ с рядом распределения 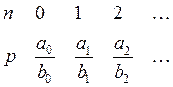
2)
Моделируем искомую СВ ![]() , например по методу
обратной функции:
, например по методу
обратной функции: 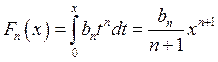 ,
, 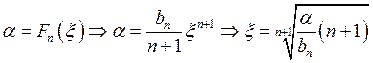
7. (е)
Написать алгоритм моделирования случайной величины ![]() с
плотностью
с
плотностью ![]() , где
, где ![]() , по
методу исключения.
, по
методу исключения.
Найдем коэффициент С из соотношения 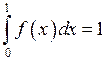 :
:
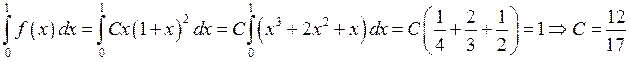
Выясним поведение функции на интервале ![]() :
:
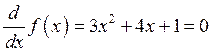 тогда
тогда 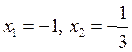 и
на последнем промежутке функция возрастает, следовательно максимальным будет
значение функции при
и
на последнем промежутке функция возрастает, следовательно максимальным будет
значение функции при ![]() , т.е.
, т.е. 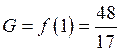
Алгоритм:
1)
Моделируем две СВ ![]() и
и ![]()
2)
Если ![]() , то
, то ![]() , иначе
на шаг 1
, иначе
на шаг 1
Событие шага 2 произойдет с вероятностью 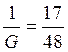 .
.
8. (г)
Составить алгоритм моделирования случайного вектора ![]() ,
распределенного в области
,
распределенного в области ![]() , с плотностью
, с плотностью ![]() .
.
Найдем коэффициент ![]() :
:
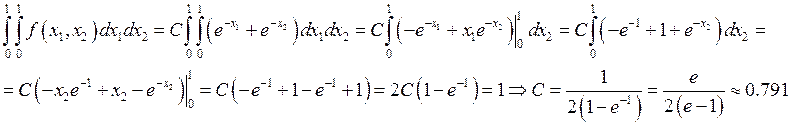
Найдем плотность распределения ![]() :
:
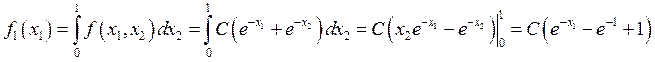
Тогда плотность условного распределения будет следующей:
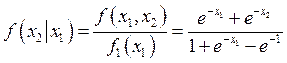
Алгоритм:
1)
Моделируем СВ ![]() с законом распределения
с законом распределения ![]()
2)
Моделируем СВ ![]() с законом распределения
с законом распределения 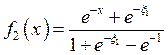
3)
Искомый случайный вектор получен: ![]()
9. (е)
Составить алгоритм моделирования случайного вектора ![]() распределенного
в области
распределенного
в области ![]() с плотностью
с плотностью ![]() по
методу исключения.
по
методу исключения.
Определим константу ![]() :
:
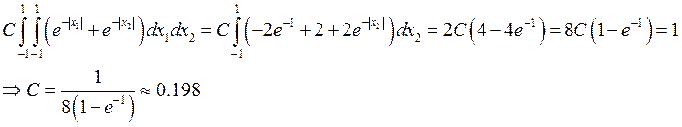
Максимум этой функции достигается в точке ![]() и равен
и равен ![]()
Алгоритм:
1)
Моделируем 3 независимых СВ ![]() и
и ![]()
2)
Если ![]() , то
, то ![]() , иначе
на шаг 1
, иначе
на шаг 1
Точка не будет исключена с вероятностью 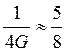 .
.
10. (в)
Найти моделирующее выражение для нормального случайного вектора ![]() с дисперсионной матрицей
с дисперсионной матрицей 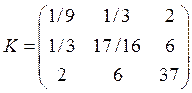 и математическим ожиданием
и математическим ожиданием 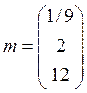 .
.
Моделирующее выражение для многомерной нормальной СВ выглядит следующим образом:
![]() , где
, где ![]() -
вектор независимых стандартных нормальных СВ.
-
вектор независимых стандартных нормальных СВ.
Необходимо посчитать коэффициенты матрицы ![]() :
:
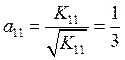 ,
, 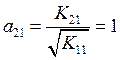 ,
, 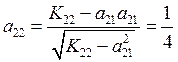 ,
,
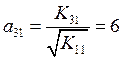 ,
, 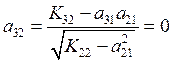 ,
, 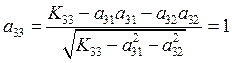
Тогда матрица 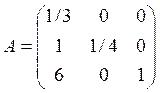 .
.
11. (5) Написать алгоритм моделирования одномерного стационарного гауссовского марковского процесса с нулевым априорным средним и одномерной корреляционной функцией вида:
![]() ,
, ![]()
Найдем условное математическое ожидание:
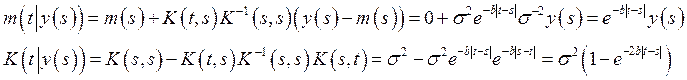
Алгоритм:
1)
Моделируем СВ ![]() ,
, ![]()
2)
Моделируем состояние в момент ![]() :
: ![]()
3)
Увеличиваем ![]() , моделируем СВ
, моделируем СВ ![]()
4)
Моделируем состояние в момент ![]() :
: ![]()
![]()
5) На шаг 3
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.