
Алгоритм GMRES, предложенный и
исследованный И.Саадом и М.Шульцем [8, 10-12, 44], для предобусловленной СЛАУ ![]() (
(![]() и
и ![]() соответственно нижняя и верхняя
треугольные матрицы неполной факторизации исходной матрицы
соответственно нижняя и верхняя
треугольные матрицы неполной факторизации исходной матрицы ![]() , т.е.
, т.е. ![]() , где
, где ![]() – матрица ошибки неполной факторизации)
выглядит следующим образом.
– матрица ошибки неполной факторизации)
выглядит следующим образом.
Выбирается начальное приближение ![]() и
полагается
и
полагается
![]() ,
, ![]() ,
, ![]() .
.
Далее для ![]() производятся следующие
вычисления.
производятся следующие
вычисления.
![]() .
.
Для ![]() (n
– размерность подпространства Крылова, которая является параметром метода)
выполняются следующие действия:
(n
– размерность подпространства Крылова, которая является параметром метода)
выполняются следующие действия:
1. Для ![]() вычисляются
вычисляются
![]() .
.
2. Определяется вектор
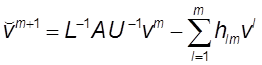 .
.
3. Находится значение
![]() .
.
4. Если ![]() , процесс заканчивается;
в противном случае определяется вектор
, процесс заканчивается;
в противном случае определяется вектор
![]() .
.
Определяется вектор 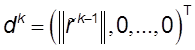 размерности
n. Вектор параметров
размерности
n. Вектор параметров ![]() формируется
как решение задачи наименьших квадратов:
формируется
как решение задачи наименьших квадратов:
![]() , после чего вычисляется новое приближение по формуле
, после чего вычисляется новое приближение по формуле
![]() и новая невязка
и новая невязка
![]() .
.
После окончания итерационного процесса необходимо вычислить решение исходной СЛАУ по формуле:
![]() .
.
Отметим, что дополнительные (сверх затрат памяти на
хранение СЛАУ) затраты памяти на реализацию GMRES с
предобусловливанием неполным разложением составляют 5 вещественных векторов.
Это рекуррентно вычисляемые векторы ![]() ,
, ![]() а также (n+1)
дополнительных векторов
а также (n+1)
дополнительных векторов ![]() , используемые для
хранения информации на протяжении одной итерации, а также 2 вспомогательных
вектора для промежуточных вычислений. Размерность векторов равна размерности
СЛАУ. Заметим, что при больших значениях n
затраты памяти на хранение
, используемые для
хранения информации на протяжении одной итерации, а также 2 вспомогательных
вектора для промежуточных вычислений. Размерность векторов равна размерности
СЛАУ. Заметим, что при больших значениях n
затраты памяти на хранение ![]() становятся
сопоставимыми с затратами памяти на хранение конечноэлементной СЛАУ.
становятся
сопоставимыми с затратами памяти на хранение конечноэлементной СЛАУ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.