Автоматическое доказательство теорем

МО РФ

НГТУ

Кафедра прикладной математики и информатики

Лабораторная работа №6

“Автоматическое доказательство теорем“

по предмету: Системы искусственного интеллекта

Факультет: ПМи

Группа: ПМ-93

Студенты: Исаева А.В., Щербакова Н.В., Шишкин Р.Н.

Преподаватель: Целебровская М.Ю.

Новосибирск 2003

Цель работы

Изучение машинных методов доказательства теорем для простых формальных систем

Задание

§  Рассмотреть заданную формальную систему и сформулированную в рамках данной системы теорему. Доказать эту теорему «вручную».

§  Написать программу автоматического доказательства теорем на Прологе, используя основные свойства среды Пролога – поиск с возвратом и унификацию.

§  Использовать метод Сиклосси-Маринова  (реализовать соответствующую эвристику) для ограничения пространства поиска доказательства.

§  Ввести в программу возможность вывода хода доказательства.

Рассматриваются следующие шесть правил вывода:

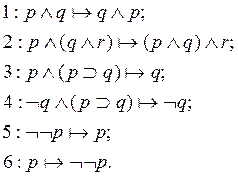
Требуется доказать теорему:

Доказательство: .

Анализ задачи

Для обеспечения нормальной работы программы доказательства теорем необходимо произвести переупорядочивание заданных правил. Это связано с тем, что некоторые правила преобразуют выражение так, что к результату может быть применимо то же самое правило (такие правила называются экстенсивными), и использование таких правил порождает бесконечное множество формул, поэтому их применение должно быть как-то ограничено. Также некоторые из правил составляют группу взаимообратных, что тоже может привести к бесконечной процедуре поиска, поэтому в предикатах вводится дополнительное ограничение на последовательность применения таких правил. Ниже приведены переупорядоченные правила

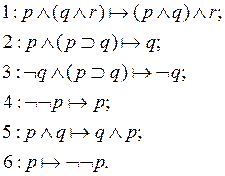
Сиклосии и Маринов предложили рассматривать экстенсивные правила только тогда, когда обойтись без них невозможно и в таком случае эти правила применяются не более одного раза для уровня текущего поиска, а полный поиск по всем другим правилам отсекается.

Тестовые примеры

1. 

Выражение:        con(impl(var("s"),no(var("t"))),var("t"))

Доказательство:

Правило 1: con(impl(var("s"),no(var("t"))),var("t")) =>

con(var("t"),impl(var("s"),no(var("t"))))

Тождество: var(s) => var(s)

Тождество: var(t) => var(t)

Правило 6: var("t") => no(no(var("t")))

Правило 4.1: con(no(no(var("t"))),impl(var("s"),no(var("t")))) => no(var("s"))

Ответ:      no(var("s")).

2. 

Выражение:       con(con(var("a"),var("b")),impl(con(var("a"),var("b")),var("q")))

Доказательство:

Тождество: var(q) => var(q)

Правило 3: con(con(var("a"),var("b")),impl(con(var("a"),var("b")),var("q"))) => var("q")

Ответ:      var("q").

3. 

Выражение:

con(impl(var("t"),con(impl(con(var("a"),var("b")),var("q")),con(var("a"),var("b")))),var("t"))

Доказательство:

Правило 1:

con(impl(var("t"),con(impl(con(var("a"),var("b")),var("q")),con(var("a"),var("b")))),var("t")) => con(var("t"),impl(var("t"),con(impl(con(var("a"),var("b")),var("q")),con(var("a"),var("b")))))

Правило 1: con(impl(con(var("a"),var("b")),var("q")),con(var("a"),var("b"))) =>

con(con(var("a"),var("b")),impl(con(var("a"),var("b")),var("q")))

Тождество: var(q) => var(q)

Правило 3: con(con(var("a"),var("b")),impl(con(var("a"),var("b")),var("q"))) => var("q")

Правило 3: con(var("t"),impl(var("t"),var("q"))) => var("q")

Ответ:        var("q").

4. 

Выражение:       con(var("a"),var("b"))

Доказательство:

Правило 1: con(var("a"),var("b")) => con(var("b"),var("a"))

Тождество: var(a) => var(a)

Тождество: var(b) => var(b)

con(var("a"),var("b")) => con(var("a"),var("b"))

Правило 6: con(var("a"),var("b")) => no(no(con(var("a"),var("b"))))

con(var("a"),var("b")) => con(var("b"),var("a")

Ответ:         no(no(con(var("a"),var("b")))).

5. 

Выражение:          con(no(con(var("p"),impl(var("p"),var("q")))),impl(var("p"),var("q")))

Доказательство:

Правило 1:

con(no(con(var("p"),impl(var("p"),var("q")))),impl(var("p"),var("q")))  => con(impl(var("p"),var("q")),no(con(var("p"),impl(var("p"),var("q")))))

Тождество: var(q) => var(q)

Правило 3: con(var("p"),impl(var("p"),var("q"))) => var("q")

no(con(var("p"),impl(var("p"),var("q")))) => no(var("q"))

impl(var("p"),var("q")) => impl(var("p"),var("q"))

Правило 6: impl(var("p"),var("q")) => no(no(impl(var("p"),var("q"))))

impl(var("p"),var("q")) => impl(var("p"),var("q"))

Тождество: var(p) => var(p)

Правило 4: con(no(var("q")),impl(var("p"),var("q"))) => no(var("p"))

Правило 1:

con(no(var("q")),impl(var("p"),var("q"))) => con(impl(var("p"),var("q")),no(var("q"))

Ответ:         no(var("p")).

Текст программы

DOMAINS

EXPR=con(EXPR,EXPR);  % конъюнкция

impl(EXPR,EXPR);      % импликация

no(EXPR);             % отрицание

var(symbol).          % переменная

PREDICATES

nondeterm reduce(EXPR,EXPR,integer)

CLAUSES

% терминальное тождество: p -> p, где p - переменная

reduce(var(X),var(X),_):- nl, write("Тождество: "), write("var("),

write(X), write(") => var("), write(X), write(")").

% терминальное тождество: ^p -> ^p, где p - переменная

reduce(no(var(X)),no(var(X)),_):- nl, write("Тождество: "), write("no(var("),

write(X), write(")) => no(var("), write(X), write("))").

% p & (q & r) -> (p & q) & r

reduce(con(P,con(Q,R)),con(con(P1,Q1),R1),N) :- nl,write("Правило 2: "),  

write("con("), write(P), write(",con("), write(Q),write(","), write(R),  

write(")) => con(con("), write(P), write(","),write(Q), write("),"), write(R),

write(")"),reduce(P,P1,0), reduce(Q,Q1,0), reduce(R,R1,0).

% p & (p > q) -> q

reduce(con(P,impl(P,Q)),Q1,N):- reduce(Q,Q1,0),

nl, write("Правило 3: "), write("con("), write(P), write(",impl("),

write(P), write(","), write(Q1), write(")) => "), write(Q1).

% ^q & (p > q) -> ^p

reduce(con(no(Q),impl(P,Q)),no(P1),N):- reduce(P,P1,0),nl, write("Правило 4: "), write("con(no("), write(Q), write("),impl("),write(P1), write(","), write(Q), write(")) => "), write("no("), write(P1), write(")").

% q & (p > ^q) -> ^p

reduce(con(Q1,impl(P,no(Q1))),no(P1),N):- reduce(P,P1,N),

reduce(Q1,no(no(Q1)),0), nl, write("Правило 4.1: "), write("con(no(no("),  

write(Q1), write(")),impl("), write(P1), write(",no("), write(Q1),

write("))) => "), write("no("), write(P1),write(")").

% ^^p -> p

reduce(no(no(P)),P1,N):- reduce(P,P1,0), nl, write("Правило 5: "),

write("no(no("), write(P1),write(")) => "),  write(P1).

% ^P->^P' (P->P')

reduce(no(P),no(P1),N):- reduce(P,P1,0),  nl, write("           "),

write("no("), write(P),write(") => no("),  write(P1), write(")").

% p & q -> q & p

reduce(con(P,Q),X,0):- nl, write("Правило