




Моделирование информационных процессов в условиях
внешних воздействий на систему
аспирант МГИУ Иванец Е.М.
Автоматизированное прогнозирование состоянии системы путем моделирования происходящих в ней информационных процессов заключается в преобразовании входных данных представленных в виде функциональных моделей (например, IDEF, UML или в терминах описания CPN) в раскрашенную сеть Петри с последующим моделированием и анализом этой сети.
Однако, данная модель недостаточно адаптирована под изменения условий функционировании самой моделируемой системы. Часто изменения внешних условий носят редкий характер типа удара или встряски, и оперативная реакция модели на такие события может играть ключевую роль в функционировании системы
Предлагаемый ниже подход является расширением базовой модели сети Петри и позволяет оперативно менять функционирование CPN, моделируя состояния системы после внешнего воздействия. Характеристикой данного подхода является изменение в рамках модельного времени декларации сети, без изменения структуры самой модели.
Рассмотрим пример раскрашенной CPN, на объект моделирования которой воздействуют внешние события, и возможные варианты поведения CPN в соответствии с новыми «экстремальными» условиями,
Декларации, сети:
L= {a, b, c, d ..., h}, L — множество цветов.
Функция срабатывания перехода (f1):
переход срабатывает, если для каждой из его входных позиций выполняется условие Ni >= Кi,
где Ni — число маркеров в i-й входной позиции; Кi — число дуг, идущих от i-й позиции к переходу.
При срабатывании перехода число маркеров в i-й входной позиции уменьшается на Кi , а в j-й выходной позиции увеличивается на Mj, где Mj — число дуг, связывающих переход с j-й позицией. Чтобы переход мог сработать, все переменные, входящие в пусковую функцию перехода и выражений на связанных с ними дугах должны получить значения.
Декларации сети меняются, если происходит некоторое, непредусмотренное в первоначальной модели событие, которое меняет функцию перехода Ai (рис.1):
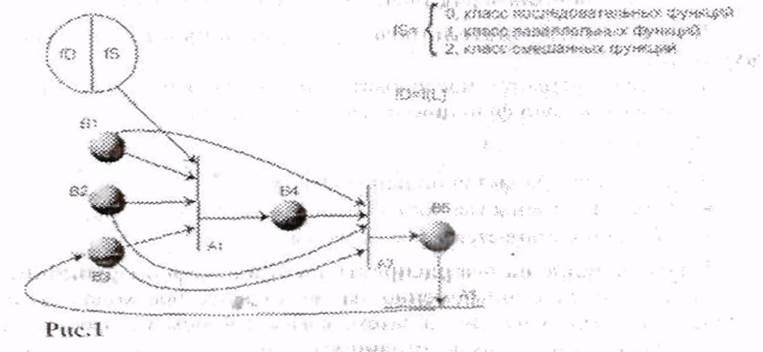
Новые декларации сети
К предыдущим декларациям добавляется функция срабатывания перехода fD=f(L). Рассматриваемое событие несет в себе новые условия функционирования системы и состоит из двух компонент: норой функции перехода fD и функции распространения fS.
Примером fD могут служить любые функции. Зависящие от компонентов сети Петри. Например, «умножитель» (умножает количество фишек определенного цвета), «заменитель» (заменяет цвета фишек с одного на другой.), «фильтр» (блокирует определенные цвета).
В данном случае fD является функцией цвета:
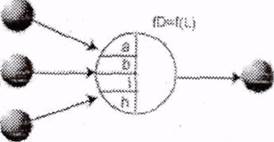
Функция распространения fS может иметь классы и подклассы, которые описаны ниже. Одной из задач САПР, использующей предлагаемую технологию, заключается в классификации внешнего воздействия с целью выработки дальнейших действий fS может принимать ряд значений в зависимости от класса:
Класс последовательного распространения пусковой функции:
fS распространяется последовательно, в каждый момент времени Т, меняя пусковую функцию на каждом переходе.
Подклассы:
• fS распространяется по направлениям дуг;
• fS распространяется против направлений дуг;
• fS распространяется в обе стороны
Класс параллельного распространения пусковой функции:
fS появляется одновременно на нескольких переходах меняя пусковую функцию на них, а затем, в каждый момент времени Т, распространяется по дугам к соседним переходам.
Подклассы:
• fS распространяется по направлениям дуг;
• fS распространяется против направлений дуг;
• fS распространяется в обе стороны;
• fS появляется на всех переходах сети одновременно (простейший случай — просто замена функции перехода в СП)
Особый интерес представляет класс смешанного распространения пусковой функции:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.