


Пусть задан ориентированный граф G = (X,U), где X = {x1, x2, … , xn} – множество вершин графа, U = {u1, u2, … , um} – множество дуг uij=(xi, xj), xi, xj Є X, причем каждой дуге приписан неотрицательный вес (число, большее или равное нулю) С = {c1, c2, … ,cm}, ci >= 0. Необходимо найти кратчайший путь (длина пути определяется как сумма весов дуг, входящих путь) от xs (начальная вершина) к xt (конечная вершина).
Наиболее эффективный алгоритм решения задачи о кратчайшем пути для двух заданных вершин в ориентированном графе первоначально дал Дейкстра[10]. В общем случае этот метод основан на приписывании вершинам временных пометок, причем пометка вершины дает верхнюю границу длины пути от начальной вершины к конечной вершине. Эти пометки (их величины) постепенно уменьшаются с помощью некоторой итерационной процедуры, и на каждом шаге итерации точно одна из временных пометок становится постоянной. Последнее указывает на то, что пометка уже не является верхней границей, а дает точную длину кратчайшего пути от начальной вершины к конечной вершине. Опишем этот алгоритм.
Совершенно очевидно, что данная задача имеет решение, если существует путь от вершины xs к вершине xt,
Граф задается матрицей весов С = ║сij║ (i,j = 1, 2, … , n), сij >= 0, причем если сij > 0, то существует дуга от вершины xs к вершине xt.
1. Приписываем вершине xs (начальная вершина) постоянную метку l(xs)* = 0. Всем остальным меткам приписываем временные метки, равные бесконечности l(xi) = ∞ (i = 1, 2, … , n; i ≠ s). Вектор меток будет равен L = (0*, ∞, … , ∞) (звездочкой отмечена постоянная метка). Вектор пути D = (xs). Пусть xk = xs.
2. Для всех вершин xi, для которых cki > 0 и имеющих временные метки, изменить метки в соответствии со следующим выражением: l(xi) = min [l(xi), l(xk) + c(xk, xi)]. Если таких вершин xi нет, то задача не имеет решения, т.е. пути от вершины xs к вершине xt в заданном графе не существует (конец алгоритма).
3. В векторе пометок L найти временную метку с минимальным значением l(xj) = min [l (xi)] (это значение не должно быть равным бесконечности). Данную метку сделать постоянной l*(xj). Вершину xj заносим в вектор пути D = (xs, … , xj). Положить xk = xj.
4. Если xk = xt, то конец алгоритма, иначе перейти к пункту 2.
Значение метки l*(xt) будет равно значению кратчайшего пути от вершины xs к вершине xt в заданном графе.
Если необходимо найти все кратчайшие пути от вершины xs ко всем остальных вершинам, то в пункте 4 нужно всегда переходить к пункту 2 до тех пор, пока или все метки станут постоянными (в этом случае граф является связным), или нет временных меток, не равных бесконечности (в этом случае граф является несвязным, причем постоянные метки определяют компоненту связности с вершиной xs).
Пример
Рассмотрим граф, изображенный на рис. 5.1, где каждое неориентированное ребро рассматривается как пара противоположно ориентированных дуг равного веса
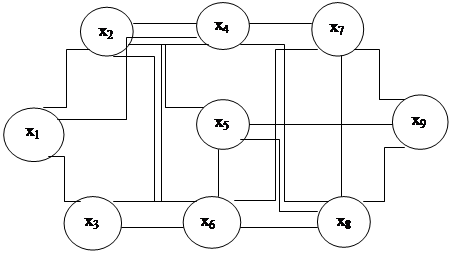 |
Рис.5.1
Матрица весов С приведена ниже:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
|
|
x1 |
0 |
2 |
3 |
13 |
0 |
0 |
0 |
0 |
0 |
|
x2 |
0 |
0 |
0 |
5 |
10 |
3 |
0 |
0 |
0 |
|
x3 |
0 |
0 |
0 |
9 |
0 |
12 |
0 |
0 |
0 |
|
x4 |
13 |
5 |
0 |
0 |
0 |
0 |
9 |
8 |
0 |
|
x5 |
0 |
0 |
0 |
0 |
0 |
6 |
0 |
13 |
12 |
|
x6 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
8 |
0 |
|
x7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
|
x8 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
7 |
|
x9 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
7 |
0 |
|
Итерация |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
x1 |
0* |
||||||||
|
x2 |
2 |
2* |
|||||||
|
x3 |
3 |
3 |
3* |
||||||
|
x4 |
∞ |
7 |
7 |
7 |
7* |
||||
|
x5 |
∞ |
12 |
12 |
12 |
12 |
12 |
12 |
12* |
|
|
x6 |
∞ |
5 |
5 |
5* |
|||||
|
x7 |
∞ |
∞ |
∞ |
8 |
8 |
8* |
|||
|
x8 |
∞ |
∞ |
∞ |
13 |
13 |
13 |
13 |
13 |
13* |
|
x9 |
∞ |
∞ |
∞ |
∞ |
∞ |
10 |
10* |
||
Только что описанный алгоритм Дейкстры применим лишь в том случае, когда cij ≥ 0 для всех i и j. Однако если матрица C является матрицей стоимостей, то дуги, приносящие доход, должны иметь отрицательные «стоимости». В этом случае для нахождения кратчайших путей между вершиной s и всеми другими вершинами можно воспользоваться описанной ниже процедурой. Этот метод также является итерационным и основан на пометках вершин, причем в конце k-й итерации пометки равны длинам тех кратчайших путей (от s ко всем остальным вершинам), которые содержат не более k +1 дуг. В отличие от алгоритма Дейкстры никакая из пометок во время этого процесса не рассматривается как окончательная
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.