Средние величины. Исчисление средней арифметической взвешенной в дискретном ряду распределения

В настоящей работе мы предприняли попытку показать на практических примерах методы статистических исследований хозяйственной деятельности предприятий и учреждений с использованием средних величин. Все примеры – условные. Материал, несущий иллюстративный характер показан на рисунках

3.1. Исчисление простой среднеарифметической по индивидуальным данным

Средняя величина является обобщающей характеристикой совокупности однотипных явлений по изучаемому признаку. Она должна вычисляться с учётом экономического содержания определяемого показателя, поскольку каждый показатель имеет своё, только ему присущее содержание, например:

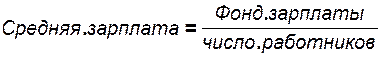
Средняя арифметическая простая (невзвешенная х) равна сумме отдельных значений признака (иначе - варианты х) делённой на число этих значений (п):

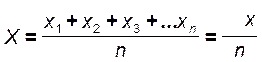
Пример. Имеются следующие данные о количестве изготовленных изделий специалистом фирмы за одну смену.

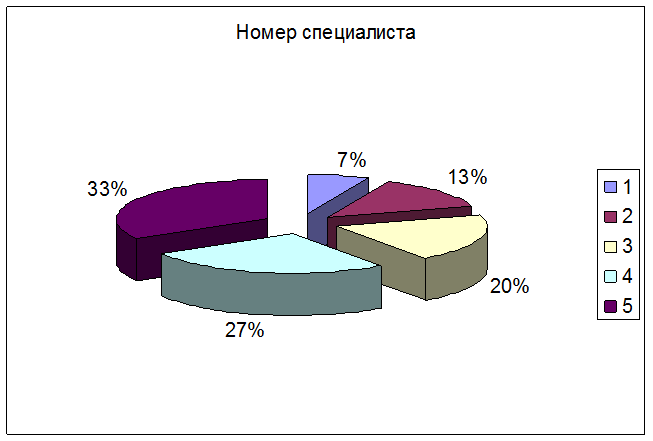
Рисунок. Изготовлено разными специалистами продукта за одну смену.

В данном примере - варьирующий признак - количество изделий, изготовленных за смену. Численные значения признака (30,31,29,...) называют вариантами. Определим среднее арифметическое:

3.2. Исчисление средней арифметической взвешенной в дискретном ряду распределения

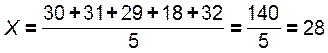
Простая средняя арифметическая применяется в тех случаях, когда имеются отдельные значения признака, т.е. данные не сгруппированы. Если данные представлены в виде рядов распределения или группировок, то средняя исчисляется иначе.

Пример. Имеются следующие данные о заработной плате специалистов фирмы района.

Таблица 15 Заработная плата специалистов фирмы

По данным дискретного ряда распределения видно, что одни и те же значения признака (варианта) встречаются несколько раз. Так, варианта Х1 встречается в совокупности три раза, а варианта Х3-шесть раз и т.д.

Число одинаковых значений признака в рядах распределения называется частотой или весом и обозначается символом f.

Исчислим среднюю заработную плату одного специалиста Х:

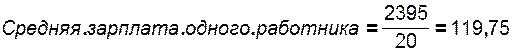
Фонд заработной платы по каждой группе специалистов равен произведению варианта на частоту, а сумма этих произведений даёт общий фонд заработной платы. В соответствии с этим, расчёты можно представить в общем виде:

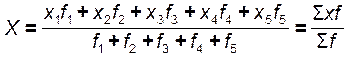
Полученная формула называется средней арифметической взвешенной. Из неё видно, что средняя зависит не только от значений признака, но и от их частот, т.е. от состава совокупности, от её структуры.

3.3. Исчисление средней арифметической взвешеннойв интервальном ряду распределения с закрытыми и отрытыми интервалами

Статистический материал в результате обработки может быть представлен не только в виде дискретных рядов распределения, но и в виде интервальных вариационных рядов с закрытыми или с отрытыми интервалами.

Рассмотрим расчёт средней арифметической для таких рядов.

Имеются следующие данные.

Таблица 16.Ассортимент конфет в киосках второй категории

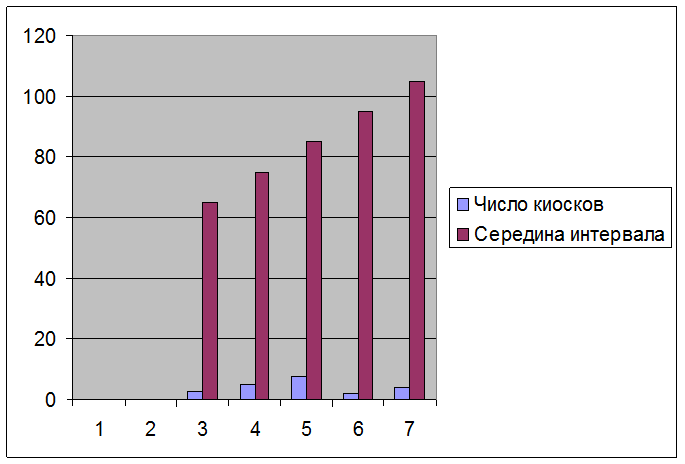
Рисунок распределение киосков и значений серединных интервалов изучаемого признака.

Вычислим средний ассортимент на одном киоске. В данном ряду варианты осреднённого признака (ассортимент) представлены не одним числом, а в виде интервала "от - до". На киосках группы № I ассортимент от 60 до 70 наименований, во второй группе - от 70 до 80 наименований и т.д. Таким образом, каждая группа ряда распределения имеет нижнее и верхнее значение варианта, или закрытые интервалы.

Исчисление средней по сгруппированным данным производится по формуле средней арифметической взвешенной:

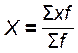
Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения интервала. Так, для первой группы она равна:

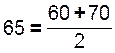
Дальнейший расчет производится обычным методом определения средней арифметической взвешенной:

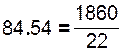
Итак, средний ассортимент конфет в киосках -  85 наименований