Плотность тока ионной эмиссии. Формула Бома. Ток ионной эмиссии с учетом ионизации в предслое

Плотность тока ионной эмиссии

Формула Бома

При подаче на граничащий с плазмой электрод потенциала, отрицательного по сравнению с потенциалом плазмы, из нее начинают вытягиваться ионы, а электроны отталкиваются и в тормозящем поле распределяются по закону Больцмана. В результате непосредственно вблизи электрода формируется слой, в котором преобладает ионный заряд, а граница плазменной области, в которой концентрации ионов и электронов одинаковы, отодвигается от электрода на расстояние равное длине слоя. Обозначим через n_b плотность плазмы на границе плазма – слой и примем упрощающее допущение, что все ионы пересекают эту границу с одинаковой скоростью v_b и имеют энергию . Углубившись в слой на некоторое небольшое расстояние  ионы увеличат свою энергию на -е (стоит знак минус так как перепад потенциала  отрицательный и, соответственно, -е будет положительным) и будут иметь скорость . Следовательно их концентрация станет несколько меньше

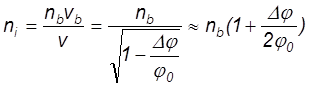
Концентрация электронов также уменьшится

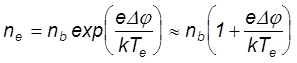
причем она должна уменьшится сильнее, чем концентрация ионов, поскольку мы приняли, что вблизи электрода формируется слой с преобладанием ионного заряда. Тогда получаем, что должно выполняться условие

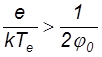
Или иначе энергия иона на границе плазма – слой должна отвечать условию

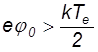, а скорость v_b должна быть больше, чем (kT_e/M)^1/2. Записанное условие известно как критерий Бома.

Для того, чтобы объяснить каким образом ионы приобретают на выходе из плазмы такую скорость было предложено разделить плазменную область на область невозмущенной плазмы с концентрацией n₀, в которой электрическое поле отсутствует, и область возмущенной плазмы, в которой выполняется условие квазинейтральности, но тем не менее существует электрическое поле, ускоряющее ионы в сторону границы плазма – слой. Эту область возмущенной плазмы Бом предложил называть предслоем. Если принять, что в предслое сосредоточен перепад потенциала , разгоняющий ионы до скорости (kT_e/M)^1/2, а электроны распределены по Больцману, то получаем

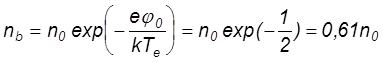,  а для плотности тока ионной эмиссии получаем формулу Бома

. 

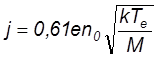Однако проделанный вывод содержит явное противоречие. Действительно если считать, что в предслое происходит только ускорение ионов при отсутствии процессов ионизации, то из уравнения непрерывности мы получаем, что на границе между невозмущенной плазмой и предслоем должен протекать такой же ток, как и на границе предслой-слой, и должно выполняться

j=еn_bv_b=еn₀v₀

где v₀ –скорость ионов на границе невозмущенная плазма – предслой. Мы получаем, что в невозмущенной плазме, где электрическое поле отсутствует, ионы должны тем не менее каким - то образом набирать скорость . Кроме того именно с этой скоростью ионы должны попадать в предслой, в то время, как мы только что приняли, что перепад потенциала в предслое должен обеспечивать ускорение ионов от 0 до (kT_e/M)^1/2. Снять эти противоречия можно, если считать, что в предслое происходит не только ускорение ионов, но и их генерация.

Ток ионной эмиссии с учетом ионизации в предслое

Запишем уравнение непрерывности

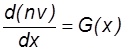
где G – число ионов, генерируемых внешним источником, если плазма