Высокочастотный разряд. Раcчет ВАХ межэлектродного промежутка с однородной плазмой, страница 2

где S - площадь электродов, e - диэлектрическая проницаемость диэлектрика, а Е_д - напряженность электрического поля в нем. В последнее выражение следовало бы вставить еще напряженность поля в металле но примем что она равна 0 так как проводимость металла существенно выше проводимости плазмы и тем более проводимости диэлектрика.

Применяя к тем же границам уравнение непрерывности получаем

dQ/dt = i,                                   (1)

dQ₁/dt = jS = I                           (2)

где  i - ток во внешней цепи , I - ток в плазме. Напряжение подаваемое на электроды делится между плазмой и двумя диэлектрическими слоями

U = Ed + 2E_дl

где  l  - толщина диэлектрика. Если выразить напряженность поля в диэлектрике из граничных условии, а в плазме из закона Ома то можно переписать полученное соотношение в следующем виде

U =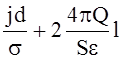

С другой стороны подставляя в первое из граничных условий

Е - eЕ_д = 4pQ₁/S

второе

eЕ_д =4pQ/S

получим

Е - 4pQ/S =  4pQ₁/S

откуда

Е=4p(Q+Q₁)/S

и для тока в плазме получаем

I = jS = sES = 4ps(Q+Q₁)

Вводя следующие обозначения

R = d/(sS) - сопротивление плазменного столба

C = S/4pd  - емкость плазменного столба

C_д = eS/4pl - емкость диэлектрика перепишем уравнения для напряжения на электродах и тока в плазме в следующем виде

U = 2Q/C_д + IR                              (3)

I = (Q + Q₁)/RC                              (4)

Считая, что на электроды подано известное напряжение

U = U_asinwt

мы имеем систему 4 уравнений для 4 неизвестных  i, I, Q, Q₁.  Подставляя (4) в (3) и дифференцируя получим

U_awcoswt = 2i/C_д +(dI/dt)R            (3’)

Дифференцируя (4) получим

dI/dt = (i+I)/RC                         (4э)

Выражая  i  из (3’) получаем

i = (U_awcoswt - (dI/dt)R)C_д/2               (5)

и подставляя в (4’) получаем

dI/dt = [(U_awcoswt - (dI/dt)R)C_д/2 + I]/RC

Группируя слагаемые получаем

(RC+RC_д/2)dI/dt - I = U_awcoswt или вводя параметр

t = RC + RC_д/2

имеем

tdI/dt - I = U_awcoswt.

Интегрируя однородное уравнение получаем

I = Aexp(-t/t).

Теперь считаем, что A = A(t) и неоднородное уравнение приводится к виду

t(dA/dt)exp(-t/t) = U_awcoswt.

Дальнейшие вычисления полностью аналогичны тому что уже делалось на предыдущей лекции :  ехр переносится в правую часть и проводится интегрирование. Интеграл берется дважды по частям и после умножения найденного А(t) на ехр(-t/t) в выражениие для  I  имеются члены с затухающей экспонентой, которые отбрасываются, и без нее, которые сохраняются. Полученное выражение приводится к более компактному виду после введения обозначения

f = arctgwt

и использования формулы для синуса суммы двух углов. Окончательный результат для тока в плазме

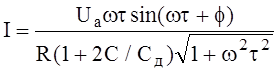
Умножая на R получим падение напряжения на плазменном столбе, а если затем еще поделить на  d  то получим напряженность поля в плазме. Однако токовый прибор включенный во внешнюю цепь покажет не  I  а  i. Вспоминая (5)

i = (U_awcoswt - (dI/dt)R)C_д/2

и вводя обозначения

t₁ = RС,  f₁ = arctgwt₁

для  i  можно получить следующее выражение

i =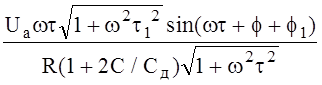

Из полученного выражения можно получить при соответствующем предельном переходе выражение для тока в случае отсутствия диэлектрика. При  l  стремящемся к 0, С_д и t стремятся к бесконечности. Тогда

2C/C_д = 0, wt(1+w²t²)^-1/2 = 1 и f = p/2

и окончательно для  i  получаем

i =

В случае оголенных электродов анализ ситуации проводится аналогичным образом, причем отсутствие диэлектрика даже несколько упрощает ситуацию. Для тока и напряженности поля в плазме и тока во внешней цепи получаются следующие соотношения

I =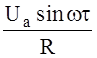

E =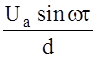

i =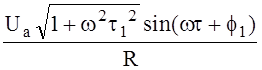

Однако для того, чтобы воспользоваться полученными выражениями, надо знать чему равно введенное нами по ходу дела сопротивление плазмы  R . Вспоминая известное выражение

j = env = enmE

и закон Ома

j = sE

получаем

s = enm.

Таким образом для нахождения s, а значит и R  надо знать концентрацию плазмы. Считая что ионизация уравновешивается рекомбинацией запишем следующее уравнение для  n

<n_i>n = bn²

Следовательно

n = <n_i>/b, где

<n_i> =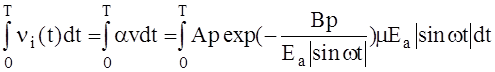

При анализе пробоя мы считали что частицы даже при высоких давлениях исчезают из промежутка в результате диффузии, а рекомбинацию не учитывали, так как при зажигании разряда концентрация заряженных частиц мала и квадратичный член  n² не играет роли. При горении разряда концентрация велика и ситуация меняется. Основным процессом гибели частиц по крайней мере при высоких давлениях становится рекомбинация, а диффузией частиц к стенкам можно пренебречь.