Генерация однородной плазмы. Профиль концентрации плазмы при различных условиях ионизации, страница 2

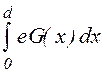j_c =                                                                     (6)

была одинаковой. Пусть

G₁ = j_c / ed,                                                                           (7)

G₂ = 3j_c / ed.                                                                       (8)

В плазме вместо уравнения Пуассона будем использовать условие квазинейтральности

n_i = n_e = n                                                                           (9)

Комбинируя уравнения (1), (2), (3) и (9) можно для концентрации плазмы получить следующее уравнение

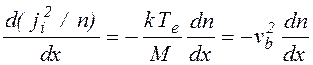                                       (10)        где

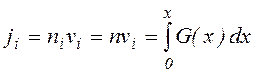.                                              (11)

Интегрируя (10) в пределах от 0 до х получаем

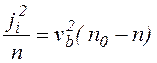.                                                               (12)            

После умножения обеих частей (12) на n и деления на  получаем для обезразмеренной концентрации n/n₀ квадратное уравнение, решение которого имеет следующий вид

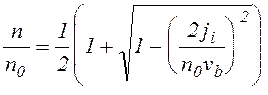.                                            (13)

Вообще говоря перед квадратным корнем может стоять и знак минус, но тогда получаем функцию не спадающую, а растущую по мере приближения к поглощающей стенке, что вряд ли имеет физический смысл. Что же касается выбранного решения, то и оно имеет физический смысл лишь до тех пор пока j_i < n₀v_b/2. В точке х, в которой j_i становится равной n₀v_b/2 производная dn/dx обращается в бесконечность. Эту точку можно считать границей квазинейтральной плазмы. Пренебрегая толщиной приэлектродного слоя пространственного заряда и считая, что нарушение условия квазинейтральности происходит в точке x = d, получим связь между концентрацией плазмы в центре системы и плотностью тока на стенке

j_с = 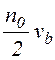.                                                                          (14)

Используя полученное соотношение для обезразмеренной концентрации в первом случае получаем

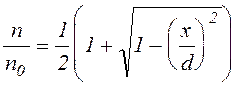,                                                  (16)

а во втором

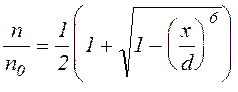.                                                  (17)

Графики обеих функций приведены на рисунке. В обоих случаях концентрация  имеет  максимум  в  центре  системы  и  постепенно спадает к периферии, однако во втором случае, когда ионизация идет неравномерно и преимущественно сосредоточена на периферии системы, спад существенно более пологий и плазма близка к однородной в большей части промежутка.

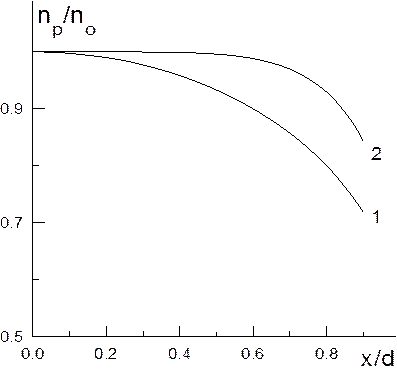
Рис. Распределение концентрации для случаев:  1 - G ~const и 2 - G ~ x².

Обсудим вопрос, а можно ли при каком – то распределении ионизации получить равномерную концентрацию во всем промежутке от одной стенки до другой. В рамках рассмотренной модели на этот вопрос, видимо, следует ответить отрицательно, так как условие dn/dx=0, выполняющееся в области однородности, очевидно, несовместимо с условием dn/dx=, выполняющимся на стенке. Таким образом, вблизи поглощающей стенки всегда будет довольно резкий спад концентрации, но, тогда, возникает вопрос, а возможно ли получить идеально однородную плазму хотя бы в некоторой, причем желательно как более широкой области [-x₀,x₀]. Анализируя выражение (13) можно прийти к несколько озадачивающему выводу, что для этого необходимо, чтобы плотность ионного тока была равна 0 и соответственно ионизация в пределах этой области должна отсутствовать. Это недостаток одномерной модели. В реальной ситуации, когда размеры системы в направлении перпендикулярном оси х не являются бесконечными, происходит уход частиц и в этом направлении.  Тогда в этой области необходима ионизация, компенсирующая этот уход.

Оставаясь в рамках одномерной задачи приближенно учтем уход частиц в продольном направлении приняв, что он происходит с Бомовской скоростью . Тогда система уравнений примет  следующий вид

n_e = n₀exp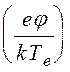,                                                   (5.2.2)

n_e=n_i=n,                                                                          (5.2.3)

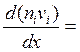G(x) - 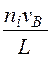,                                             (5.2.4)

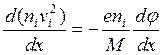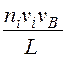 -                                     (5.2.5)

Анализ записанной системы уравнений показывает, что получение однородной плазмы с концентрацией n₀  в центральной области возможно при двух различных уровнях ионизации в этой области

G = n₀v_B /L                                                              (5.2.6)

и

G = n₀v_B / 2L.                                                          (5.2.7)

В первом случае все ионы, образовавшиеся в центральной области, уходят из нее в продольном направлении и величина радиального потока в этой области равна 0, а во втором случае эмиссия из центральной области идет как за счет ионизации в ней так и за счет того, что в центральную область входит поток ионов с периферии системы. Для реализации второй ситуации необходимо, чтобы распределение концентрации и потенциала на периферии было немонотонным и имело максимум.  При дальнейшем уменьшении ионизации ниже указанных уровней должны формироваться распределения с минимумом в центре системы.