Эмиссия электронов из тлеющих разрядов с осциллирующими электронами, страница 10

Различие между потенциалом коллектора, при котором происходит насыщение электронного тока, и плавающим  потенциалом,  при котором ионный и электронный токи на коллектор равны, составляет 40-50 В, что несколько превышает значение

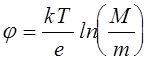
(по проведенным оценкам Т=5-6 эВ), которое должно получаться в отсутствие влияния  электронной эмиссии на разряд. Такое различие может объясняться повышением потенциала приосевой плазмы при отборе электронов.
Снижение приосевой электронной концентрации вызывает уменьшение ее радиального грандиента, а повышение потенциала уменьшение радиальной напряженности электрического поля, поскольку в отражательном разряде с полым катодом потенциал приосевой  плазмы ниже потенциала анода. Оба этих фактора, так же  как  и  обнаруженные в условиях электронной эмиссии  снижение  частоты  вращения плазменного факела и подавление вращательной неустойчивости, уменьшают перенос электронов на анод поперек  магнитного поля и обеспечивают переключение электронного тока с анода на коллектор. Таким образом, в отражательном разряде с  полым катодом механизм переключения  является  многофакторным и  существенно более сложным, чем рассмотренный в [123-124].

6.4. Змиссионные свойства плазмы, ограниченной прикатодной областью разряда низкого давления

В настоящем разделе анализируются особенности  извлечения  электронов  через  цилиндрический  эмиссионный  канал  в  катоде  (см.рис.6.15) при горении разряда низкого давления типа тлеющего. Поскольку величина катодного падения потенциала  в  таких  разрядах обычно на порядок выше анодного  и  достигает  сотен  вольт, змиссией через потенциальный барьер, создаваемый катодным падением, можно пренебречь при наличии открытой плазменной  поверхности. Тогда эмиссионный ток определяется соотношением

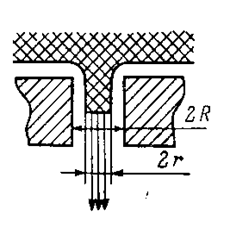
Рис.6.15. Эмиссионный канал.

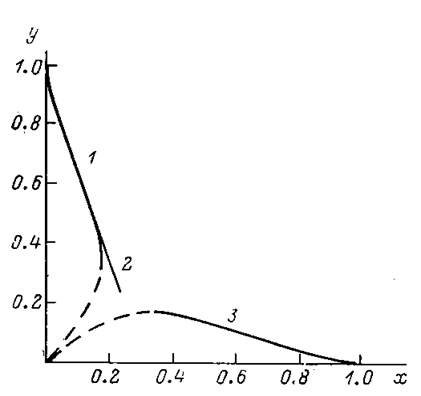
Рис.6.16. Функции:1 - y = f ^-1(х), 2 - y = 0.9 - 2.9x, 3 - y = f(х)

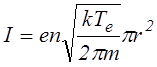,                                                        (6.4.1)

где r – радиус открытой поверхности плазмы (см. рис.6.15)

В разряде низкого давления движение ионов в катодном падении можно считать бесстолкновительным и для расчета r воспользоваться "законом 3/2" для цилиндрического ионного слоя. Определяя плотность выходящего из плазмы ионного тока по известной  формуле Бома и задавая связь между концентрацией плазмы и током разряда в виде

n = aI_d                                                                          (6.4.2)

(обычно а - соnst, в общем случае а = а (I_d) ), преобразуем "закон 3/2" к следующему виду

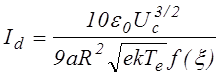                                                 (6.4.3)

где U_c – катодное падение потенциала, R – радиус эмиссионного  канала, f(x)=xb²(1/x), x=r/R, b² – трансцендентная табулированная функция [24].

Разрешая (6.4.3) относительно xи подставляя полученное выражение в (6.4.1), получим

,                                                (6.4.4)

где

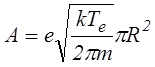,                                                            (6.4.5)

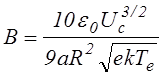,                                                           (6.4.6)

f ^-1  – функция, обратная к f. Функция f  немонотонная, поэтому обратная функция является двузначной (см. рис.6.16). Для
определения x необходимо использовать верхнюю ветвь, так как плазма в  цилиндрическом канале неустойчива при малых r (см. главу 3).

Для расчета параметров А и В необходима модель разряда, которая позволяла бы определить значения а, Т_е, U_c при известном I_d, но для использовавшегося в экспериментах эмиттера на  основе  отражательного  разряда с полым катодом такая модель до настоящего времени не  разработана. Однако известно [2], что величины а, Т_е, U_c  слабо  меняются при изменении I_d, поэтому можно рассмотреть, в какой степени экспериментальные эмиссионые характеристики описываются функциями вида (6.4.4) при постоянных А и В, подобранных  путем последовательных приближений. Из рис.6.17 видно, что расчетные линии вполне удовлетворительно описывают  ход  экспериментальных характеристик причем, несмотря на довольно сложную функциональную зависимость эти характеристики  можно  с  хорошей  точностью аппроксимировать линейными функциями вида