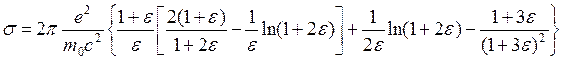Взаимодействие γ-излучения и рентгеновского излучения с веществом, страница 2

                                                                                                                                            (16.5)

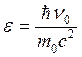.                                                                                                                                            (16.6)

16.1.3. Фотоэффект.

Фотоэффектом называется процесс взаимодействия γ – квантов, при котором вся его энергия расходуется на ионизацию атома (сообщается кинетическая энергия электрону, а γ – квант исчезает):

E _γ = E_e +I_i,                                                                                                                                            (16.7)

где E_e – кинетическая энергия выбитого электрона, I_i – потенциал ионизации i-той оболочки атома.

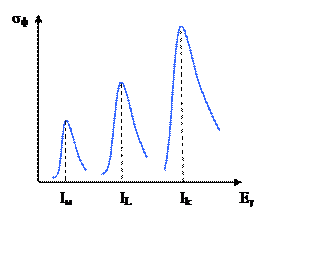
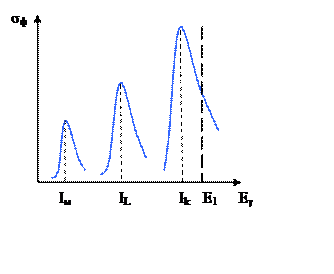
Рис. 16.1. Сечение фотоэффекта.

Чем меньше энергия связанного электрона, тем мене вероятен фотоэффект.

Электроны, вызванные мягким излучением (Eγ << mc²), движутся главным образом в направление электрического вектора, т.е. перпендикулярно направлению движения кванта. С увеличением энергии распределение электронов вытягивается в направление движения γ – квантов.

                                                                                                                                          (16.10)

16.1.4. Образование электрон - позитронных пар.

При достаточно высокой энергии γ – кванта (E _γ >> m₀c²) наряду с фотоэффектом и эффектом Комптона может иметь место четвёртый вид взаимодействия – образование электрон-позитронных пар.

Такой процесс теоретически обоснован в 1929 году П.Дираком в результате анализа релятивистского квантово – механического уравнения для электрона.

Процесс образования пар не может происходить в пустоте, т.к. это будет противоречить закону сохранения энергии. Надо, кроме того, чтобы соблюдался ещё и закон сохранения импульса.

1. Если процесс образования пары (электрона и позитрона) происходит в кулоновском поле ядра, то энергия отдачи ядра будет весьма малой, так что пороговая (критическая) энергия γ-кванта может быть получена из уравнения баланса энергии

                                     ,                                         (16.11)

если положить E_k=0, тогда

                                                  (16.12)

,  = 0,51 МэВ  и  , следовательно, E_γ,c=1,02 МэВ

2. При образовании электрон-позитронной пары в кулоновском поле электрона будет весьма существенной энергия отдачи электрона, что приводит к удвоению пороговой энергии. 2Eγ,c=2,04 МэВ.

В первом случае энергия отдачи ядра настолько мала, что в камере Вильсона следы ядра не видны (в настоящее время вместо камер Вильсона используют ионизационные камеры с электромагнитными датчиками углов и компьютерной записью траекторий):

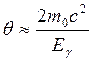.                                                                                                                                          (16.13)

Частицы летят под углом друг к другу.

Во втором случае кроме электрона и позитрона виден электрон отдачи. Такое трехэлектронное событие обычно называют тройником. Сечение образования пары сложно зависит от Z и E_γ (Z – заряд ядра). При E_γ > 10 МэВ сечение образования пар на электронах составляет ~ 1% общего сечения в тяжёлых элементах и - около 10% в лёгких.

                                                                                                                                          (16.14)

Сечение образования электрон-позитронных пар в кулоновском поле электрона примерно на три порядка меньше сечения их образования в поле ядра.

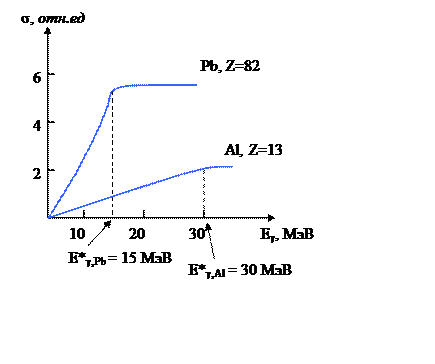
Рис. 17.1. Сечения образования электрон-позитронных пар для Al и Pb

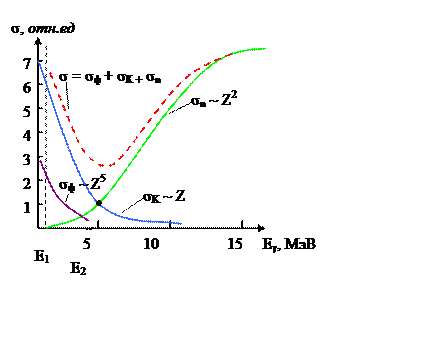
При взаимодействии γ – квантов с веществом надо рассматривать три основных процесса (фотоэффект, комптоновское рассеяние и образование электрон-позитронных пар), плюс томпсоновское рассеяние в случае мягкого рентгена (при малых E):

                                                                         (17.4)

3)

E_γ < E₁ – фотоэффект

E₁ < E_γ < E₂ – эффект Комптона

E_γ > E₂ – образование электрон – позитронных пар

Рис. 16.2. Сечения основных процессов