Расчет коэффициентов уравнений множественной регрессии в виде линейной (аддитивной) и нелинейной (мультипликативной) моделей

Задача.

Рассчитать коэффициенты уравнений множественной регрессии в виде линейной  (аддитивной) и нелинейной (мультипликативной) моделей, определяющих зависимость объёма продаж от стоимости основного капитала и численности промышленно-производственного персонала фирмы.

W=a₀+a₁F+a₂L —аддитивная модель

—мультипликативная модель

F – стоимость основного капитала

L – численность персонала (человек)

W – объём продаж

 Коэффициенты уравнений регрессии получить методом наименьших квадратов. Для сведения мультипликативной модели к аддитивной использовать логарифмирование. Для получения исходных данных использовать датчик случайных чисел. Число предприятий равно 15.

Выполнить проверку уравнений регрессии с помощью подстановки средних значений  факторов (F,L) по группе из 15 предприятий, а также по значениям коэффициентов множественной корреляции.

 По результатам анализа выбрать наиболее подходящий вид модели по условию максимального коэффициента множественной корреляции. И сделать вывод  на основании анализа коэффициентов  регрессии и коэффициентов эластичности.

Исходные данные               табл.3.3

N	W=W1+W2	F	L
1	6,6786	0,8502	110,9370
2	7,8700	1,1810	62,1444
3	7,7547	0,9887	110,2668
4	11,0187	1,2539	132,3508
5	12,9153	1,6301	77,4097
6	7,3316	0,8226	132,2821
7	5,9761	0,8953	80,8721
8	6,7929	0,6251	150,8709
9	11,9459	1,3568	130,3890
10	16,2236	1,7648	126,1189
11	12,2955	1,5168	96,3799
12	6,3225	0,8090	109,6749
13	9,8281	1,0980	138,0848
14	12,1421	1,2649	155,1850
15	8,7024	1,1461	98,8075

Технология решения задачи в Еxcel.

1.Составление исходных таблиц:

q  В стандартной панели инструментов выбираем команду вставка функции, а затем функцию – случайное число

q  Численность персонала найдем по формуле: L=120(-lnE_1i)^0,25

q  Объем продаж, зависящий от численности персонала, найдем по формуле: W₁=3(-lnE_1i)^0,4 

Численность персонала          табл.3.1

q  Стоимость основного капитала найдем по формуле: F=1,2(-lnE_2i)^0,25

q  Объем продаж, зависящий от стоимости основного капитала, найдем по формуле: W₂=7(-lnE_2i)^0,4

Стоимость основного капитала   табл.3.2

2.Расчет аддитивной модели (W=a₀+a₁F+a₂L):

q  Для нахождения а₀,а₁,а₂ составим следующую систему уравнений:

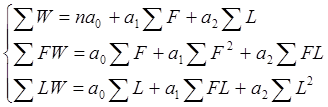
q  Для нахождения сумм составим таблицу на основе исходных данных:

Расчет коэффициентов уравнения регрессии для аддитивной модели                                                                                                                                                               табл.3.4

q  Найдем коэффициентыа₀,а₁,а₂ через определители. Для этого в стандартной панели инструментов выбираем команду вставка функции, а затем функцию –определитель матрицы

q   По полученной формуле (W= -5.474 + 9.257F + 0.039L) найдем теоретическое распределение продаж

Распределение объема продаж   

                              табл.3.5

q  Для расчета коэффициента корреляции в стандартной панели инструментов выбираем команду вставка функции, а затем функцию – коэффициента корреляции

3.Расчет мультипликативной модели ()

q  Для нахождения составим следующую систему уравнений:

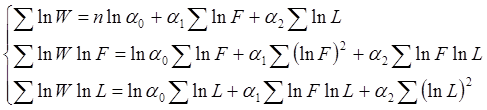
q  Для нахождения сумм составим таблицу на основе исходных данных:

Расчет коэффициентов уравнения регрессии для мультипликативной модели                                                                                                                                       табл.3.6

q  Остальные расчеты производятся аналогично аддитивной модели

4. По результатам проверки наиболее подходящим является линейная модель (по максимальному коэффициенту множественной корреляции R_а= 0,993, R_м=0,957).