Разработка модели интерактивного описания специализированных знаков безопасности

вещественные оценки принадлежности объекта х к классу

 C при условии I(x). В качестве окончательного решения классификации принимается класс с* (I (x)) = argmax r(I(x)). Тривиальная схема системы распознавания изображения специализированных знаков безопасности в рамках описанной модели на рис.2

Рис. 2 –Тривиальная схема распознавания знаков безопасности

Если исключить из рассмотрения процесс валидации результатов распознавания и процесс обучения параметров системы распознавания (в случае, если для решения задачи классификации используются методы машинного обучения, к примеру, искусственные нейронные сети), и рассматривать непосредственно процесс распознавания, то такая система распознавания является статической и не предлагает обратных связей.

Рассмотрим теперь задачу распознавания х в видеопотоке. Источником видеопотока является некоторое захватывающее устройство, представляющее последовательность различных кадров, каждый из которых является независимым изображением объекта х. В условиях фиксированного количества кадров можно рассматривать задачу распознавания объекта в видеопотоке как статистическую систему, аналогичную представленной на рис.3, но с более сложной моделью входа. Тогда последовательность из N кадров можно рассматривать как множество изображений объекта х: I (x) = { (x), (x),.., (x)}. При этом модель выхода системы остается неизменной.

2.2 Разработка методов и алгоритмов анализа и распознавания специализированных знаков безопасности

Обучение нейронной сети

·  Обучение нейронной сети- это процесс, в котором параметры нейронной сети настраиваются посредством моделирования среды, в которую эта сеть встроена. Тип обучения определяется способом подстройки параметров. Различают алгоритмы обучения с учителем и без учителя. Процесс обучения с учителем представляет собой предъявление сети выборки обучающих примеров. Каждый образец подается на входы сети, затем проходит обработку внутри структуры НС, вычисляется выходной сигнал сети, который сравнивается с соответствующим значением целевого вектора, представляющего собой требуемый выход сети.

Для того, чтобы нейронная сети была способна выполнить поставленную задачу, ее необходимо обучить (см.рис.2.1). Различают алгоритмы обучения с учителем и без учителя.  Процесс обучения с учителем представляет собой предъявление сети выборки обучающих примеров. Каждый образец подается на входы сети, затем проходит обработку внутри структуры НС, вычисляется выходной сигнал сети, который сравнивается с соответствующим значением целевого вектора, представляющего собой требуемый выход сети. Затем по определенному правилу вычисляется ошибка, и происходит изменение весовых коэффициентов связей внутри сети в зависимости от выбранного алгоритма. Векторы обучающего множества предъявляются последовательно, вычисляются ошибки и веса подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемо низкого уровня.

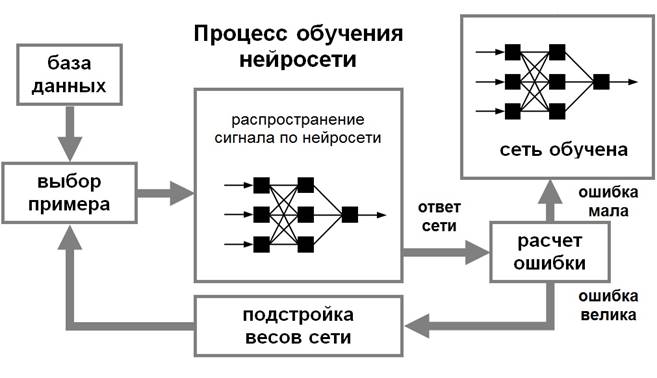
Рис. 2.1. Иллюстрация процесса обучения НС

При обучении без учителя обучающее множество состоит лишь из входных векторов. Обучающий алгоритм подстраивает веса сети так, чтобы получались согласованные выходные векторы, т.е. чтобы предъявление достаточно близких входных векторов давало одинаковые выходы. Процесс обучения, следовательно, выделяет статистические свойства обучающего множества и группирует сходные векторы в классы. Предъявление на вход вектора из данного класса даст определенный выходной вектор, но до обучения невозможно предсказать, какой выход будет производиться данным классом входных векторов. Следовательно, выходы подобной сети должны трансформироваться в некоторую понятную форму, обусловленную процессом обучения. Это не является серьезной проблемой. Обычно не сложно идентифицировать связь между входом и выходом, установленную сетью. Для обучения нейронных сетей без учителя применяются сигнальные метод обучения Хебба и Ойа.

Математически процесс обучения можно описать следующим образом. В процессе функционирования нейронная сеть формирует выходной сигнал Y, реализуя некоторую функцию Y = G(X). Если архитектура сети задана, то вид функции G определяется значениями синаптических весов и смещенной сети.

Пусть решением некоторой задачи является функция Y = F(X), заданная параметрами входных-выходных данных (X¹, Y¹), (X², Y²), …, (X^N, Y^N), для которых Y^k = F(X^k) (k = 1, 2, …, N).

Обучение состоит в поиске (синтезе) функции G, близкой к F в смысле некоторой функции ошибки E.

Если выбрано множество обучающих примеров – пар (X^N, Y^N) (где k = 1, 2, …, N) и способ вычисления функции ошибки E, то обучение нейронной сети превращается в задачу многомерной оптимизации, имеющую очень большую размерность, при этом, поскольку функция E может иметь произвольный вид обучение в общем случае – многоэкстремальная невыпуклая задача оптимизации.

Для решения этой задачи могут использоваться следующие (итерационные