Рассматриваемая модель полета является в высшей степени идеализированной. В частности, мы совершенно не учитываем возможные манипуляции с рулями самолета и не принимаем в расчет изменения числа оборотов двигателя. В действительном полете возможны компромиссные решения между скоростью и крутизной траектории.
При
выполнении эксперимента фиксируем характеристики самолета 
и изменяем начальную
скорость и угол полета.
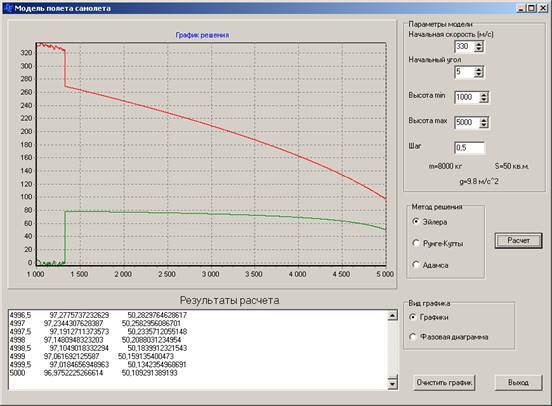
Рисунок.2. Окно выполнения программы для случая начальная скорость близка к скорости звука и почти горизонтальный угол наклона.
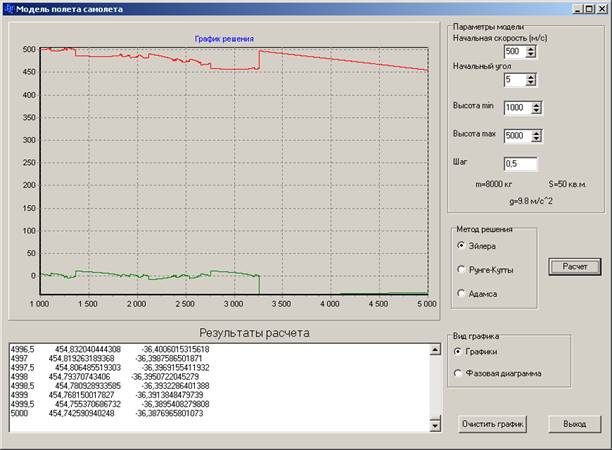
Рисунок.3. Окно выполнения программы для случая начальная скорость более скорости звука и почти горизонтальный угол наклона.
Рисунок.4. Окно выполнения программы для случая начальная скорость близка к скорости звука и угол наклона 450.
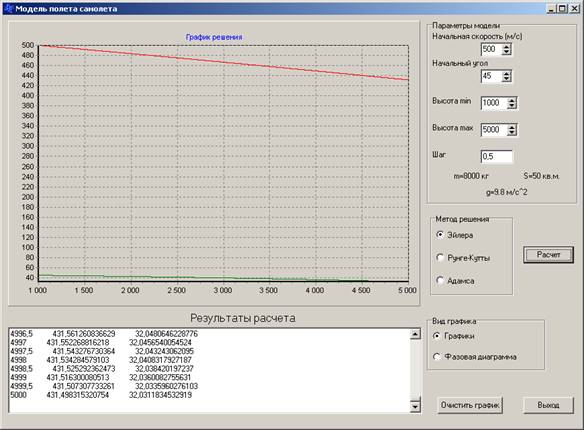
Рисунок.5. Окно выполнения программы для случая начальная скорость больше скорости звука и угол наклона 450.
Рисунок.6. Окно выполнения программы для случая начальная скорость близка к скорости звука и угол наклона 850.
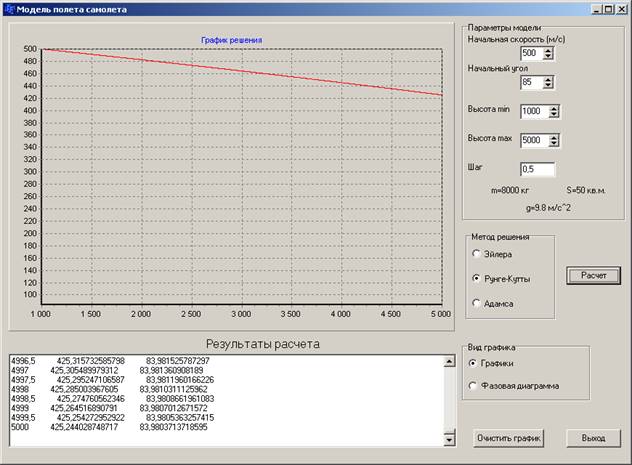
Рисунок.7. Окно выполнения программы для случая начальная скорость близка к скорости звука и угол наклона 850.
Часто
для анализа решений удобнее строить не временные решения, а зависимости между
искомыми величинами. Плоскость 
называется
фазовой плоскостью, а совокупность точек, построенных на этой плоскости, по
результатам решения называется фазовой кривой. Если рассматриваемые движения
являются периодическими, то фазовые кривые являются замкнутыми. Если найденная
функция зависит от трех переменных, то строится трехмерное фазовое пространство
и проводится анализ проекций фазовых траекторий на фазовых координатных
плоскостях.
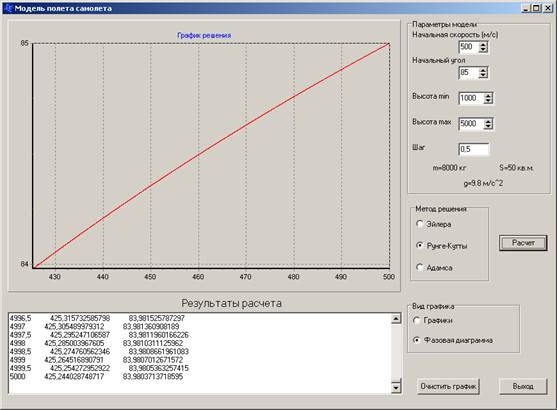
Рисунок.8. Зависимость между скоростью и углом наклона.
Таким образом, видим что наша модель в целом согласуется с теоретической, но дает недостаточно корректные результаты при задании граничных условий.
Начальные условия установлены среднему:
1. Метод Рунге-Кутты. До 3000 м кривые согласуются с теорией, а выше заметны небольшие флюктуации (см. рисунок 9):
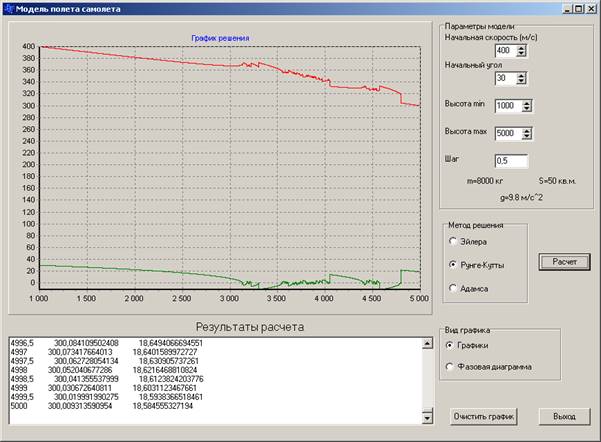
Рисунок.9. Окно выполнения программы при выборе метода Рунге-Кутты.
2. Метод Адамса. Получена ожидаемая форма графиков более точно рассчитано изменение скорости полета (см. рисунок 10):
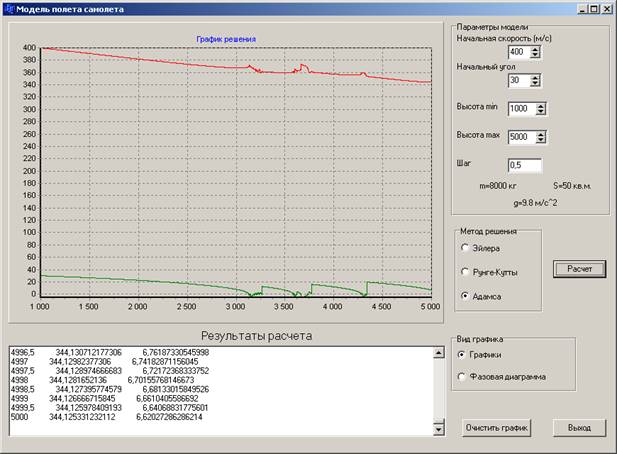
Рисунок.10. Окно выполнения программы при выборе метода Адамса.
3. Метод Эйлера. Наблюдается наименьшее отклонение от ожидаемого результата (см. рисунок 11):
Рисунок 11. Окно выполнения программы при выборе метода Эйлера.
Таким образом, при одинаковых начальных условиях метод Эйлера дал лучшие результаты при отображении динамики процесса, хотя и наименее точен по сравнению с другими методами, при этом метод Адамса дает лучшие результаты по сравнению с методом Рунге-Кутта.
1. Выбираем первоначально шаг интегрирования h=100, наблюдаем следующий вид графиков (см. рисунок 12):
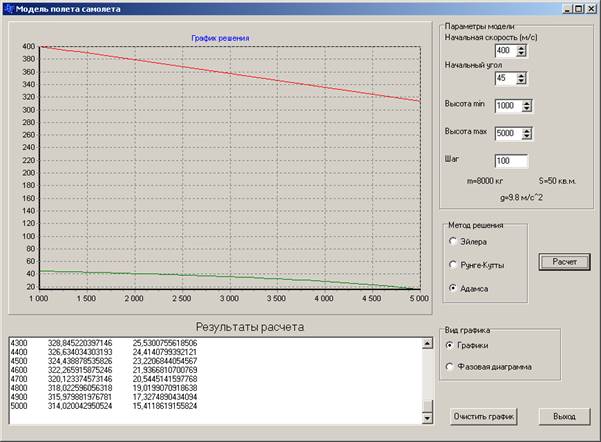
Рисунок 12. Окно выполнения программы при выборе метода Адамса при шаге интегрирования 100
2. Шаг уменьшили в 100 раз (h=1), результат выполнения программы получился только немного более точным (см. рисунок 13):
Рисунок 13. Окно выполнения программы при выборе метода Адамса при шаге интегрирования 1
3. Дальнейшее уменьшение шага не изменяет характер процесса, кроме значительного увеличения времени выполнения (см.рисунок 14):
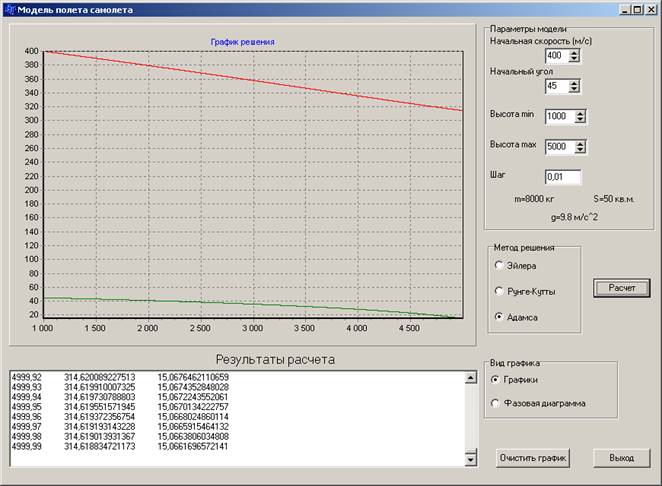
Рисунок 13. Окно выполнения программы при выборе метода Адамса при шаге интегрирования 0,01
Следовательно, шаг h=1 является для метода Адамса оптимальным, а решение системы ОДУ при указанном шаге будет являться устойчивым.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.