Преимущества LDPC-кодов, их применение и перспективы развития

ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ В СОВРЕМЕННЫХ СИСТЕМАХ ПЕРЕДАЧИ ДАННЫХ.РЕАЛИЗАЦИЯ КОДЕРА И ДЕКОДЕРА LDPC (LOW-DENSITY PARITY-CHECK)

Оглавление

Введение. 3

1 Практическая часть. 8

2 Преимущества LDPC-кодов, их применение и перспективы развития. 16

3 Исследование принципов реализации ldpc кодека на плис. 19

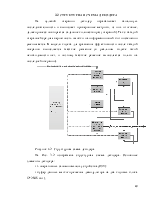
3.1 Описание кодера и декодера. 20

3.2 Структурная схема кодера на ПЛИС.. 22

3.2 Структурная схема декодера. 23

3.3 Моделирование. 24

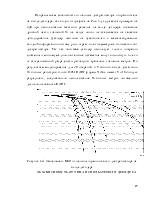
3.4 Зависимость от количества итераций декодирования. 25

3.5 Зависимость от наличия дискретизатора на входе декодера. 26

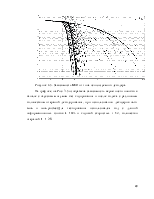
3.6 Зависимость от типа используемого декодера. 27

Заключение. 29

Список литературы.. 30

Введение

В настоящее время происходит интенсивное развитие различных цифровых систем передачи данных, таких как космическая, спутниковая, мобильная связь и др. Все подобные системы используют для передачи данных беспроводные каналы, в которых на передаваемый сигнал действуют помехи различной физической природы. Это приводит к тому, что принятые данные с достаточно большой вероятностью будут содержать ошибки. В то же время для многих практических приложений допустима лишь очень небольшая доля ошибок в обрабатываемых дискретных данных. В результате возникает проблема обеспечения надежной передачи цифровой информации по каналам с шумами.

Важнейший вклад в решение данной проблемы вносит теория помехоустойчивого кодирования. На ее основе разрабатываются методы защиты от ошибок,  базирующиеся на применении помехоустойчивых кодов. Использование этих кодов позволяет получить энергетический выигрыш кодирования (ЭВК), который характеризует степень возможного снижения энергетики передачи при кодировании по сравнению с отсутствием кодирования, если достоверность передачи в обоих случаях одинакова. Этот выигрыш можно использовать для улучшения параметров и характеристик многих важных свойств систем передачи данных, например, для уменьшения размеров очень дорогих антенн, повышения дальности связи, увеличения скорости передачи данных, снижения необходимой мощности передатчика и т.д.

Сформулируем задачи, для которых найдены решения средствами помехоустойчивого кодирования:

·  кодирование для обеспечения надежной передачи в каналах передачи данных (физический уровень сети);

·  кодирование в системах с обратной связью (уровень звена передачи данных);

·  кодирование на транспортном уровне сети;

·  кодирование для защиты от несанкционированного доступа (уровень приложений);

·  кодирование для сжатия информации с потерями (уровень приложений).

На сегодняшний день теории кодирования известно много кодов и методов их декодирования, различающихся энергетическим выигрышем, вносимой избыточностью, сложностью реализации и рядом других параметров [турбо-коды, каскадные коды, низкоплотностные коды (LDPC-коды) и многие другие].  

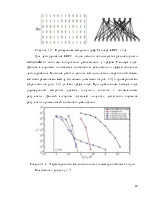
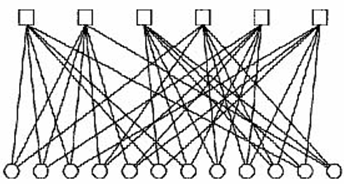
Низкоплотностные коды (LDPC). Прекрасные характеристики, получаемые при итеративном декодировании турбо кодов, стимулировали активные исследования по применению данного метода к декодированию других кодов. В результате оказалось возможным получить еще лучшие характеристики при декодировании низкоплотностных (Low Density Parity Check – LDPC) кодов [13], предложенных Галлагером еще в 1962 г. [14]. Данные коды представляют собой линейные блоковые (N, K) коды, задаваемые с помощью проверочной матрицы H, характеризуемой относительно малым числом единиц в строках и столбцах. Часто LDPC коды удобно представлять с помощью графа Таннера, в котором для представления строк и столбцов проверочной матрицы используются определенным образом связанные между собой битовые и проверочные узлы. Например, для кода с матрицей H граф Таннера представлен на рисунке

Среди LDPC кодов выделяют регулярные и нерегулярные коды [15-17].

Проверочная матрица первых характеризуется тем, что во всех столбцах и строках имеется одинаковое число единиц λ и ρ соответственно. В нерегулярных LDPC кодах данное свойство не соблюдается, и веса столбцов и строк описываются с помощью функций λ(i) и ρ(i), задающих долю столбцов и строк с весом i. Для примера на рис. 10 представлена проверочная матрица и граф Таннера для нерегулярного LDPC кода, в котором λ(2) = 8/9, λ(3) = 1/9, ρ(3) = 1/5, ρ(4) = 4/5.

а)

б)

Рисунок 0.1 - Проверочная матрица и граф Таннера регулярного LDPC кода

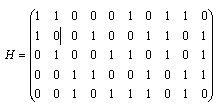
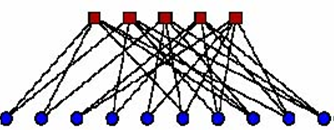
Рисунок 0.2 - Проверочная матрица и граф Таннера нерегулярного LDPC кода

Для декодирования LDPC кодов обычно используется разновидностьитеративного декодирования, называемая алгоритмом распространения надежности (Belief Propagation – BP) [18], работающего с графом кода. Также возможно применение различных модификаций данного алгоритма, характеризуемых меньшей сложностью реализации. В основе работы данных методов лежит итеративный обмен мягкими