Нестационарная теплопроводность.Тепловой расчёт экономайзера

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

МАГНИТОГОРСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Г.И.НОСОВА

КАФЕДРА ТЕПЛОТЕХНИЧЕСКИХ И ЭНЕРГЕТИЧЕСКИХ СИСТЕМ

КУРСОВАЯ РАБОТА

ПО ТЕПЛОМАССООБМЕНУ

МАГНИТОГОРСК

                                                             2010           

Металлическая заготовка, имеющая форму пластины (цилиндра), неограниченной длинны, с начальной температурой , нагревается в печи, температура которой  поддерживается постоянной до конечной температуры по оси заготовки . Считая длину (и высоту) заготовки большими по сравнению с толщиной, определить:

1.  Время нагревания заготовки до данной конечной температуры;

2.  Температуры на оси и на поверхности заготовки для различных моментов времени (с использование монограмм Будрина);

3.  Распределение температуры по толщине заготовки для четырёх моментов времени (с использованием аналитических формул);

4.  Количество теплоты, подведённой к телу в течение всего периода нагревания (на 1  поверхности пластины или на 1  длины цилиндра);

5.  По результатам (2) и (3) построить графики.

Форма тела: ПЛАСТИНА

Материал: СТАЛЬ 40

1._Определение времени нагревания заготовки до конечной температуры

Сначала найдем из справочных таблиц теплофизические параметры пластины (теплоёмкость, коэффициент теплопроводности, коэффициент температуропроводности и плотность) при начальной температуре  и конечной температуре центра пластины , и вычислим их средние значения:

Вычислим число  и безразмерную температуру  для центра пластины в последний момент времени нагрева:

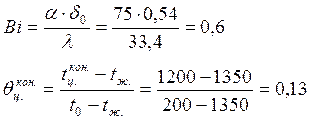
По номограмме Будрина для центра пластины определим:

Вычислим время нагревания заготовки:

2._Определение температур на оси и на поверхности заготовки для различных моментов времени

Интервал времени нагревания заготовки разобьём на несколько промежутков. Для каждого значения  вычислим время (в часах), найдём безразмерные температуры в центре и на поверхности пластины по номограммам Будрина (в зависимости от  и ). По безразмерным температурам вычислим температуры в центре и на поверхности пластины в градусах Цельсия.

Для :

1.  Время нагревания

2.  Безразмерная температура в центре пластины (определяем по соответствующей диаграмме Будрина в зависимости от  и ):

3.  Безразмерная температура на поверхности пластины (определяем по соответствующей диаграмме Будрина в зависимости от  и ):

4.  Температура на оси пластины:

5.  Температура на поверхности пластины:

Для остальных значений критерия Фурье вычисления производим по этим же формулам, результаты вычислений заносим в таблицу. 

3._Определение распределения температуры по толщине заготовки для четырёх моментов времени

При  определяем из таблиц:

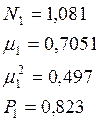
При         

При         

При         

Найдём безразмерные температуры в момент времени  

Температура для этой точки:

Для остальных точек и в другие моменты времени вычисления производим аналогичным образом, результаты записываем в таблицу.

4._Определение количества теплоты, подведённого к телу за весь период нагревания (в расчёте на 1 метр длинны пластины)

Полное количество теплоты, которое было бы подведено к пластине (на 1 метр её длинны и 1 метр ширины), если бы нагревание длилось до наступления полного теплового равновесия между пластиной и воздухом печи:

Средняя безразмерная температура в последний момент времени нагрева:

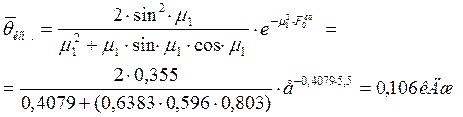
Полное количество теплоты, подведённого к пластине (на 1 метр её длинны и 1 метр ширины) за весь период нагрева:

5._Графики, построенные по данным пунктов 2 и 3

Плоская пластина  м. обтекается продольным потоком жидкости (газа) со скоростью  м/с. Температура набегающего потока . Задана температура поверхности пластины . Найти:

1.  Критическую координату  точки перехода ламинарного пограничного слоя в турбулентный;

2.  Толщины динамического  и теплового  пограничных слоёв на различных расстояниях от передней кромки поверхности;

3.  Значения местных коэффициентов теплоотдачи  на различных расстояниях от передней кромки пластины;

4.  Средние коэффициенты теплоотдачи  для участков с различными режимами течения;

5.  Построить графики , .

Жидкость: МАСЛО МК

1. Вычисление критической координаты точки перехода ламинарного пограничного слоя в турбулентный

Определим теплофизические параметры масла МК при температуре :

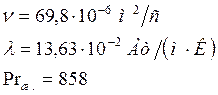
Определим число Прандтля масла МК при температуре :

Вычислим число Рейнольдса:

Критическое число Рейнольдса:

Т.к. , то режим течения в пограничном слое на конце пластины - турбулентный