|
![]()
Расчетные усилия:
![]() ,
,
![]() , где
, где ![]() –
коэффициент сочетаний нагрузок от двух кранов, зависит от режима работы
мостовых кранов, для среднего и легкого режимов (группы 1К–6К);
–
коэффициент сочетаний нагрузок от двух кранов, зависит от режима работы
мостовых кранов, для среднего и легкого режимов (группы 1К–6К);
![]() ,
,
![]() –
нормативное вертикальное усилие колеса,
–
нормативное вертикальное усилие колеса,
![]() ,
,
![]() , где
, где ![]() –
грузоподъемность крана;
–
грузоподъемность крана;
![]() ,
,
![]() –
масса крана и крановой тележки, тонн;
–
масса крана и крановой тележки, тонн;
![]() –
число колес с одной стороны ходовой части крана.
–
число колес с одной стороны ходовой части крана.
![]() ,
,
![]() .
.
Вес подкрановой балки:
![]() , где
, где
![]() –
расход стали на подкрановую балку,
–
расход стали на подкрановую балку, ![]()
![]() , где 80 – расход стали на подкрановую балку,
, где 80 – расход стали на подкрановую балку, ![]() здания
(по табл. 12.1 [3]).
здания
(по табл. 12.1 [3]).
![]() ,
,
![]() .
.
Тогда расчетные усилия:
![]() ,
,
![]() .
.
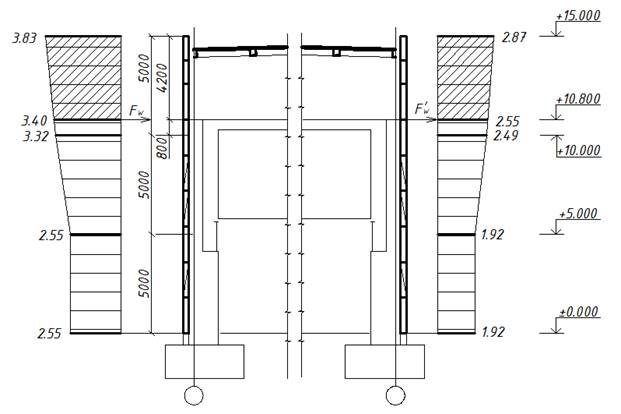
Расстояние от оси подкрановой балки до оси, проходящей через центр тяжести нижней колонны:
![]() .
.
Найдем изгибающие моменты, передаваемые силами ![]() ,
,
![]() колонне:
колонне:
![]() ,
,
![]() .
.
Нормативное значение горизонтальной силы ![]() ,
возникающей из-за перекосов крана, торможения тележки, распирающего воздействия
колес при движении по рельсам, для кранов с гибким подвесом груза равно:
,
возникающей из-за перекосов крана, торможения тележки, распирающего воздействия
колес при движении по рельсам, для кранов с гибким подвесом груза равно:
![]() ,
,
Расчетная горизонтальная сила ![]() ,
передаваемая подкрановыми балками на колонну от сил
,
передаваемая подкрановыми балками на колонну от сил ![]() :
:
![]() .
.
Ветровая нагрузка
Нормативная ветровая нагрузка зависит от района
строительства и принимается в соответствии с [2], для г. Саратова (район III):
![]() ,
также зависит от высоты над поверхностью земли. Изменение нормативной ветровой
нагрузки в зависимости от высоты проектируемого здания учитывается
коэффициентом
,
также зависит от высоты над поверхностью земли. Изменение нормативной ветровой
нагрузки в зависимости от высоты проектируемого здания учитывается
коэффициентом ![]() (табл.
Х [2] или прил. 3 [3]).
(табл.
Х [2] или прил. 3 [3]).
Расчетная линейная ветровая нагрузка, передаваемая на стойку рамы в какой-то точке по высоте определяется по формуле:
![]() , где
, где ![]() –
коэффициент надежности по ветровой нагрузке;
–
коэффициент надежности по ветровой нагрузке;
с –
аэродинамический коэффициент, принимаемый для вертикальных стен ![]() –
с наветренной стороны,
–
с наветренной стороны, ![]() –
для противоположной стороны (отсоса).
–
для противоположной стороны (отсоса).
По формуле для ![]() построим
эпюру давления ветра по высоте стены здания. Для наветренной стороны (активного
давления):
построим
эпюру давления ветра по высоте стены здания. Для наветренной стороны (активного
давления):
![]()
![]()
![]()
Для противоположной стороны (отсоса):
![]()
![]()
![]()
Промежуточные значения ![]() находят
интерполяцией.
находят
интерполяцией.
Ветровая нагрузка, действующая на участке от низа ригеля до наиболее высокой точки здания, заменяется сосредоточенной силой, приложенной в уровне низа ригеля рамы.
![]() ,
,
![]() , где
, где ![]() ,
,
![]() ,
,
![]() ,
,
![]() –
значения ветрового давления на уровне низа ригеля и верха парапета
соответственно, активного давления и отсоса;
–
значения ветрового давления на уровне низа ригеля и верха парапета
соответственно, активного давления и отсоса;
![]() –
расстояние между точкой низа ригеля и точкой верха парапета.
–
расстояние между точкой низа ригеля и точкой верха парапета.
Получив по эпюре давления ветра величины ![]() ,
,
![]() ,
,
![]() ,
,
![]() найдем:
найдем:
![]() ,
,
![]() .
.
Изгибающий момент от действия ветрового давления:
![]() , где
, где ![]() –
высота колонны,
–
высота колонны,
![]() –
эквивалентная нагрузка, равномерно распределенная по всей высоте, заменяющая
фактическую линейную в виде ломаной прямой, равная
–
эквивалентная нагрузка, равномерно распределенная по всей высоте, заменяющая
фактическую линейную в виде ломаной прямой, равная
![]() ,
,
![]() , где
, где
![]() находится
по формуле:
находится
по формуле:
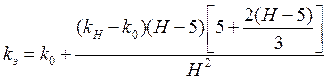 ,
,
где ![]() –
коэффициент
–
коэффициент ![]() у
поверхности земли;
у
поверхности земли;
![]() –
коэффициент
–
коэффициент ![]() на
отметке
на
отметке ![]() ;
;
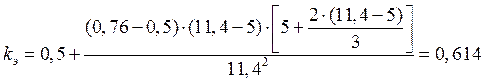 .
.
Тогда эквивалентная нагрузка:
![]() ,
,
![]() .
.
Найдем изгибающие моменты, равные
![]() ,
,
![]() .
.
|
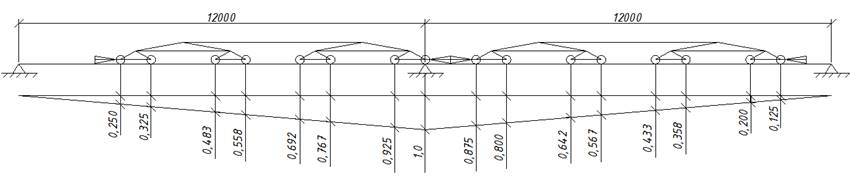
Учет пространственной работы каркаса
Учесть пространственную работу каркаса можно, определив смещение рамы в системе пространственного блока, состоящего из 5–7 плоских поперечных рам, соединенных в уровне ригеля и пространственных конструкций продольными элементами конечной жесткости.
Сложность заключается в определении величины,
характеризующей отношение смещения отдельной рамы, включенной в
пространственный каркас к ее смещению без учета работы блока. Эта величина
обозначается ![]() ,
находится по формуле:
,
находится по формуле:
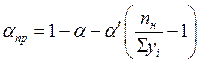 , где
, где ![]() –
число колес кранов на одной нитке подкрановых балок (
–
число колес кранов на одной нитке подкрановых балок (![]() );
);
![]() –
сумма ординат, определяемая по линиям влияния;
–
сумма ординат, определяемая по линиям влияния;
![]() ,
,
![]() –
коэффициенты упругого отпора, зависящие от параметра
–
коэффициенты упругого отпора, зависящие от параметра ![]() (табл. 12.2 [3])
характеризующего соотношения жесткостей поперечной рамы и покрытия:
(табл. 12.2 [3])
характеризующего соотношения жесткостей поперечной рамы и покрытия:
![]() , где
, где ![]() –
коэффициент приведения ступенчатой колонны к эквивалентной по смещению колонне
постоянного сечения, при жестком сопряжении ригеля с колонной:
–
коэффициент приведения ступенчатой колонны к эквивалентной по смещению колонне
постоянного сечения, при жестком сопряжении ригеля с колонной:
![]() , где
, где ![]() –
коэффициент, принимаемый при определении реакции от смещения стойки на
–
коэффициент, принимаемый при определении реакции от смещения стойки на ![]() )
по табл. 12.4 [3];
)
по табл. 12.4 [3];
![]() –
отношение суммы моментов инерции нижних частей колонн к моменту инерции
продольных связей по нижним поясам фермы и эквивалентного момента инерции
кровли (см. п. 12.3 [3])
–
отношение суммы моментов инерции нижних частей колонн к моменту инерции
продольных связей по нижним поясам фермы и эквивалентного момента инерции
кровли (см. п. 12.3 [3])
Принимаем ![]() ,
,
![]() ,
тогда:
,
тогда:
![]() .
.
![]() .
.
При ![]() Þ
Þ ![]() ,
,
![]() .
.
Из этого следует, что
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.